
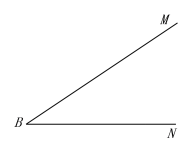
【题目】(1)如图,已知线段![]() 和
和![]() ,请在给出的图形上用尺规作出
,请在给出的图形上用尺规作出![]() ,使得:点
,使得:点![]() 在射线
在射线![]() 上,点
上,点![]() 在射线
在射线![]() 上,且
上,且![]() ,
,![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)求证:直角三角形斜边上的中线等于斜边的一半.(要求:利用(1)中的Rt![]() ,画出斜边
,画出斜边![]() 上的中线
上的中线![]() ,写出已知、求证和证明过程)
,写出已知、求证和证明过程)
![]()
科目:初中数学 来源: 题型:
【题目】中国科学技术馆有“圆与非圆”展品,涉及了“等宽曲线”的知识.因为圆的任何一对平行切线的距离总是相等的,所以圆是“等宽曲线”.除了例以外,还有一些几何图形也是“等宽曲线”,如勒洛只角形(图1),它是分别以等边三角形的征个顶点为圆心,以边长为半径,在另两个顶点间画一段圆弧.三段圆弧围成的曲边三角形.图2是等宽的勒洛三角形和圆.

下列说法中错误的是( )
A.勒洛三角形是轴对称图形
B.图1中,点A到![]() 上任意一点的距离都相等
上任意一点的距离都相等
C.图2中,勒洛三角形上任意一点到等边三角形DEF的中心![]() 的距离都相等
的距离都相等
D.图2中,勒洛三角形的周长与圆的周长相等
查看答案和解析>>
科目:初中数学 来源: 题型:
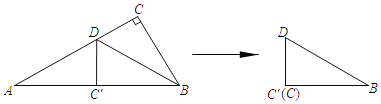
【题目】如图1,小军有一张Rt△ABC纸片,其中∠A=30°,AB=12cm.他先将该纸片沿BD折叠,使点C刚好落在斜边AB上的一点C′处.然后沿DC′剪开得到双层△BDC′(如图2).小军想把双层△BDC′沿某直线再剪开一次,使展开后的两个平面图形中其中一个是平行四边形,则他能得到的平行四边形的最大面积可为____cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
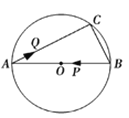
【题目】如图,AB是⊙O的直径,弦BC=6cm,AC=8cm.若动点P以2cm/s的速度从B点出发沿着B→A的方向运动,点Q以1cm/s的速度从A点出发沿着A→C的方向运动,当点P到达点A时,点Q也随之停止运动.设运动时间为t(s),当△APQ是直角三角形时,t的值为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a、b、c为常数,且
(a、b、c为常数,且![]() )的x与y的部分对应值如下表:
)的x与y的部分对应值如下表:

有下列结论:①a>0;②4a-2b+1>0;③x=-3是关于x的一元二次方程ax2+(b-1)x+c=0的一个根;④当-3≤x≤n时,ax2+(b-1)x+c≥0.其中结论正确的有____.
查看答案和解析>>
科目:初中数学 来源: 题型:
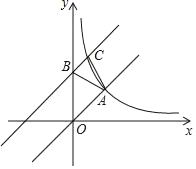
【题目】如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=![]() 的图象经过点A(2,2).
的图象经过点A(2,2).
(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于点B,与反比例函数图象在第一象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积;
(3)在第一象限内,直接写出反比例函数的值大于直线BC的值时,自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市“木兰溪左岸绿道”工程已全部建成并投入使用,10公里的河堤便道铺满了彩色的透水沥青,堤岸旁的各类花草争奇斗艳,与木兰溪河滩上的特色花草相映成趣,吸引着众多市民在此休闲锻炼、散步观光.某小区随机调查了部分居民在一周内前往“木兰溪左岸绿道”锻炼的次数,并制成如图不完整的统计图表:
居民前往“木兰溪左岸绿道”锻炼的次数统计表
锻炼次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 7 | 13 | a | 10 | 3 |
请你根据统计图表中的信息,解答下列问题:
(1)a= ,b= .
(2)请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(3)若该小区共有2000名居民,根据调查结果,估计该小区居民在一周内前往木兰溪左岸绿道”锻炼“4次及以上”的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016新疆)如图,ABCD中,AB=2,AD=1,∠ADC=60°,将ABCD沿过点A的直线l折叠,使点D落到AB边上的点D′处,折痕交CD边于点E.
(1)求证:四边形BCED′是菱形;
(2)若点P时直线l上的一个动点,请计算PD′+PB的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=16cm,BC=12cm.现有动点P从点A出发,沿线段AC向点C方向运动,动点Q从点C出发,沿线段CB向点B方向运动.如果点P的速度是4cm/s,点Q的速度是3cm/s,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为ts.
求:(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=2s时,P、Q两点之间的距离是多少?
(3)当t为多少秒时,以C、P、Q为顶点的三角形与△ABC相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com