
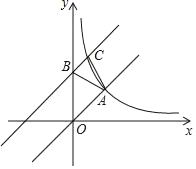
【题目】如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=![]() 的图象经过点A(2,2).
的图象经过点A(2,2).
(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于点B,与反比例函数图象在第一象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积;
(3)在第一象限内,直接写出反比例函数的值大于直线BC的值时,自变量x的取值范围.
【答案】(1)y=x,y=![]() ;(2)C(1,4);
;(2)C(1,4);![]() ;(3)0<x<1.
;(3)0<x<1.
【解析】分析:(1)将点A(2,2)代入正比例函数中即可求出k的值,再将A(2,2)代入反比例函数中即可求出m的值.
(2)由题意可知点B的坐标为(0,3),所以直线BC的解析式为y=x+3,联立直线BC的解析式与反比例函数的解析式即可求出C的坐标,连接OC,由于OA∥BC,所以△ABC的面积等于△BOC的面积.
(3)因为点C的坐标已知,在第一现象内,从图象直接观察可知x的取值范围.
详解:(1)将A(2,2)代入y=kx,
∴2k=2,
∴k=1,
∴正比例函数的解析式为:y=x
将A(2,2)代入y=![]()
∴m=2×2=4,
∴反比例函数的解析式为:y=![]() ;
;
(2)∵直线BC由直线OA向上平移3个单位所得,
∴B(0,3)
∴直线BC的解析式为:y=x+3,
联立解得:![]() 或
或![]() ,
,
∵点C在第一象限,
∴点C的坐标为(1,4)
∵OA∥BC,
∴S△ABC=S△BOC=×3×1=![]() ,
,
(3)在第一象限内,要使反比例函数y=![]() 的值大于直线BCy=x+3的值,从图象可知
的值大于直线BCy=x+3的值,从图象可知
∵点C的坐标为(1,4)
∴0<x<1



 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:
【题目】昆明市某中学“综合实践活动”棋类社团前两次购买的两种材质的围棋采购如表(近期两种材质的围棋的售价一直不变):
塑料围棋 | 玻璃围棋 | 总价(元) | |
第一次(盒) |
|
|
|
第二次(盒) |
|
|
|
(1)若该社团计划再采购这两种材质的围棋各![]() 盒,则需要多少元;
盒,则需要多少元;
(2)若该社团准备购买这两种材质的围棋共![]() 盒,且要求塑料围棋的数量不多于玻璃围棋数量的
盒,且要求塑料围棋的数量不多于玻璃围棋数量的![]() 倍,请设计出最省钱的购买方案,并说明理由.
倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△ADE中,BA=BC,DA=DE,且∠ABC=∠ADE,点E在△ABC的内部,连接EC,EB和ED,设EC=kBD(k≠0).
(1)当∠ABC=∠ADE=60°时,如图1,请求出k值,并给予证明;
(2)当∠ABC=∠ADE=90°时:
①如图2,(1)中的k值是否发生变化,如无变化,请给予证明;如有变化,请求出k值并说明理由;
②如图3,当D,E,C三点共线,且E为DC中点时,请求出tan∠EAC的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
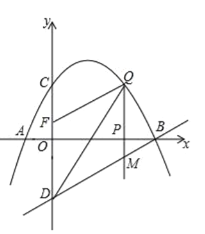
【题目】如图,已知抛物线经过点A(![]() ,0),B(4,0),C(0,2)三点,点D与点C关于
,0),B(4,0),C(0,2)三点,点D与点C关于![]() 轴对称,点P是
轴对称,点P是![]() 轴上的一个动点,设点P的坐标为(
轴上的一个动点,设点P的坐标为(![]() ,0),过点P作
,0),过点P作![]() 轴的垂线交抛物线于点Q,交直线BD于点M.
轴的垂线交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)点P在线段AB上运动的过程中,是否存在点Q,使得以B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)已知点F(0,![]() ),点P在
),点P在![]() 轴上运动,试求当
轴上运动,试求当![]() 为何值时,以D、M、Q、F为顶点的四边形是平行四边形.
为何值时,以D、M、Q、F为顶点的四边形是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
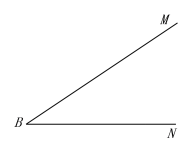
【题目】(1)如图,已知线段![]() 和
和![]() ,请在给出的图形上用尺规作出
,请在给出的图形上用尺规作出![]() ,使得:点
,使得:点![]() 在射线
在射线![]() 上,点
上,点![]() 在射线
在射线![]() 上,且
上,且![]() ,
,![]() ;(保留作图痕迹,不写作法)
;(保留作图痕迹,不写作法)
(2)求证:直角三角形斜边上的中线等于斜边的一半.(要求:利用(1)中的Rt![]() ,画出斜边
,画出斜边![]() 上的中线
上的中线![]() ,写出已知、求证和证明过程)
,写出已知、求证和证明过程)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
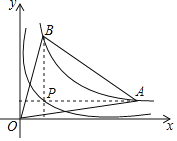
【题目】如图,点P为函数y=![]() (x>0)图象上一点,过点P作x轴、y轴的平行线,分别与函数y=
(x>0)图象上一点,过点P作x轴、y轴的平行线,分别与函数y=![]() (x>0)的图象交于点A、B,则△AOB的面积为_____.
(x>0)的图象交于点A、B,则△AOB的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
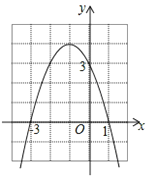
【题目】如图所示是二次函数y=ax2+bx+c的图象.下列结论:①二次三项式ax2+bx+c的最大值为4;②使y≤3成立的x的取值范围是x≤-2;③一元二次方程ax2+bx+c=1的两根之和为-1;④该抛物线的对称轴是直线x=-1;⑤4a-2b+c<0.其中正确的结论有______________.(把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
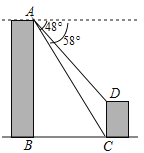
【题目】如图,甲、乙两座建筑物的水平距离BC为78m,从甲的顶部A处测得乙的顶部D处的俯角为48°,测得底部C处的俯角为58°,求乙建筑物的高度CD.(结果取整数,参考数据:tan58°≈1.60,tan48°≈1.11).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(![]() ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com