
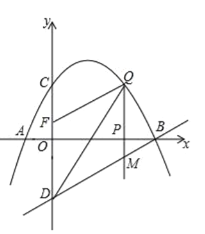
����Ŀ����ͼ����֪�����߾�����A��![]() ��0����B��4��0����C��0��2�����㣬��D���C����
��0����B��4��0����C��0��2�����㣬��D���C����![]() ��Գƣ���P��
��Գƣ���P��![]() ���ϵ�һ�����㣬���P������Ϊ��
���ϵ�һ�����㣬���P������Ϊ��![]() ��0��������P��
��0��������P��![]() ��Ĵ��߽��������ڵ�Q����ֱ��BD�ڵ�M��
��Ĵ��߽��������ڵ�Q����ֱ��BD�ڵ�M��
��1���������������ʾ�Ķ��κ����ı���ʽ��
��2����P���߶�AB���˶��Ĺ����У��Ƿ���ڵ�Q��ʹ����B��Q��MΪ��������������BOD���ƣ������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
��3����֪��F��0��![]() ������P��
������P��![]() �����˶�������
�����˶�������![]() Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
���𰸡���1��![]() ����2�����ڵ�Q��ʹ����B��Q��MΪ��������������BOD���ƣ���Q������Ϊ��3��2����
����2�����ڵ�Q��ʹ����B��Q��MΪ��������������BOD���ƣ���Q������Ϊ��3��2����![]() ��0������3����
��0������3����![]() ��
��![]() ��
��![]() ��
��![]() ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
��������
��1������������������ߵĽ���ʽΪ![]() ���ó�a��ֵ���ٴ������ʽ����
���ó�a��ֵ���ٴ������ʽ����
��2�����ڵ�Q��ʹ����B��Q��MΪ��������������BOD���ƣ����Ϊ������������ٵ���DOB=��MBQ=90��ʱ�����Եõ���MBQ�ס�BPQ���ɽ�𣬢ڵ���BQM=90��ʱ����ʱ��Q���A�غϣ���BOD�ס�BQM�伴�ɽ��
��3�����������֪��D����Ϊ��0��![]() �����õ�ֱ��BD����ʽΪ
�����õ�ֱ��BD����ʽΪ![]() ����ΪQM��
����ΪQM��![]() �ᣬP��
�ᣬP��![]() ��0������
��0������![]() ����ΪF
����ΪF![]() ��
��![]() ��D��0��
��D��0��![]() ����
����![]() �����Ե�QM=DF����
�����Ե�QM=DF����![]() ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ����ɽ��
ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ����ɽ��
�⣺��1���������߹���A��![]() ��0����B��4��0����
��0����B��4��0����
����������ߵĽ���ʽΪ![]() ��
��
�������߾�����C��0��2����
��![]() ��
��
��ã�![]() ��
��
�������߽���ʽΪ![]() ��
��
��2�����ڵ�Q��ʹ����B��Q��MΪ��������������BOD����.
��ͼ��ʾ��
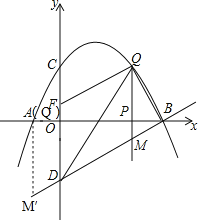
��QM��DC��
���ODB=��QMB��
���������������
�ٵ���DOB=��MBQ=90��ʱ����DOB�ס�MBQ��
��![]() ��
��
�ߡ�MBQ=90�㣬
���MBP+��PBQ=90�㣬
�ߡ�MPB=��BPQ=90�㣬
���MBP+��BMP=90�㣬
���BMP=��PBQ��
���MBQ�ס�BPQ��
��![]() ��
��
��P��![]() ��0����B��4��0����
��0����B��4��0����
��BP![]() ��
��![]() ��
��
�� ��
��
��ã�![]() ��
��
��![]() ʱ����P��Q��M�����B�غϣ����ܹ��������Σ���ȥ��
ʱ����P��Q��M�����B�غϣ����ܹ��������Σ���ȥ��
��![]() ����Q��������3��2���� ,
����Q��������3��2���� ,
�ڵ���BQM=90��ʱ����ʱ��Q���A�غϣ���BOD�ס�BQM�䣬
��ʱm=-1����Q������Ϊ��![]() ��0����
��0����
���ϣ���Q������Ϊ��3��2����![]() ��0��ʱ���Ե�B��Q��MΪ��������������BOD���ƣ�
��0��ʱ���Ե�B��Q��MΪ��������������BOD���ƣ�
��3���ߵ�D���C��0��2������![]() ��Գƣ�
��Գƣ�
���D������0��![]() ����
����
��ֱ��BD����ʽΪ![]() ��
��
���У�![]() ����ã�
����ã�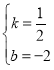 ��
��
��ֱ��BD����ʽΪ![]() ��
��
��QM��![]() �ᣬP��
�ᣬP��![]() ��0����
��0����
��Q![]() ��M
��M![]() ��
��
��![]() ��
��
��F![]() ��
��![]() ��D��0��
��D��0��![]() ����
����
��![]() ��
��
��QM��DF��
�൱QM=DF����![]() ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
��ã�m=-1��m=3��![]() ��
��![]() ��
��
��m=-1��m=3��![]() ��
��![]() ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
ʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���ʵ��ڵ�һ����x�ᡢy�����˶����ڵ�һ���ӣ�����ԭ���˶�����0��1����Ȼ����Ű�ͼ�м�ͷ��ʾ�����˶�{����0��0������0��1������1��1������1��0����}����ÿ���ƶ�һ����λ����ô��35��ʱ�ʵ�����λ�õ������ǣ�������
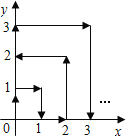
A. ��4��0��B. ��5��0��C. ��0��5��D. ��5��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ�е�С�����DZ߳�Ϊ1�������Σ���ABC�Ķ����O�㶼�������εĶ����ϣ�
��1���Ե�OΪλ�����ģ��ڷ���ͼ�н���ABC�Ŵ�Ϊԭ����2�����õ���A��B��C����
��2����A��B��C���Ƶ�B��˳ʱ����ת90����������ת��õ�����A��B��C���������A��B������ת������ɨ����ͼ�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������������ʯ�������ע���ȵ㻰���Ϊ���ѡ����������������������������࣮�������һ����������������ݣ����Ƶ�ͳ��ͼ�����£�
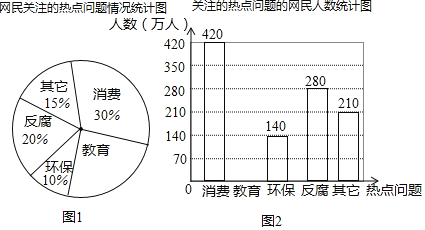
����������Ϣ����������⣺
��1�����ι����� �ˣ�����ͼ�ϲ�ȫ����ͳ��ͼ�������Ӧ���ݣ�
��2������ʯ��Լ��260���˿ڣ�����������ע�������������ԼΪ�������ˣ�
��3�����ž��õķ�չ������Խ��Խ���ӽ�����Ԥ�ƹ�ע������������ÿ����10������������������Ԥ����������й�ע�������������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������BC=6cm��AC=8cm��������P��2cm/s���ٶȴ�B���������B��A�ķ����˶�����Q��1cm/s���ٶȴ�A���������A��C�ķ����˶�������P�����Aʱ����QҲ��ֹ֮ͣ�˶������˶�ʱ��Ϊt(s)������APQ��ֱ��������ʱ��t��ֵΪ___________��
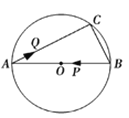
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���꾭Ӫһ��Ʒ��ˮ���������Ϊ10Ԫ/ǧ�ˣ�������Ϊ25�죬ÿ��������![]() (ǧ��)�����۵���
(ǧ��)�����۵���![]() (Ԫ/ǧ��)֮��ĺ�����ϵ��ͼ��ʾ.
(Ԫ/ǧ��)֮��ĺ�����ϵ��ͼ��ʾ.
(1)��![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
(2)����Ʒ��ˮ������Ϊ����Ԫʱ��ÿ����������õ��������
(3)��������һ���Թ�����Ʒ��ˮ��3000ǧ�ˣ�����(2)��ÿ�����������ķ�ʽ�������ۣ������ڱ������ڲ��ܼ�ʱ������ϣ����Ǿ����ڱ����ڵ����5��һ���Խ������ۣ������5��ÿǧ�����ٽ��۶���Ԫ����ȫ�����ꣿ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����������y=kx��ͼ���뷴��������y=![]() ��ͼ����A��2��2����
��ͼ����A��2��2����
��1���ֱ��������������ı���ʽ��
��2����ֱ��OA����ƽ��3����λ���Ⱥ���y�ύ�ڵ�B���뷴��������ͼ���ڵ�һ�����ڵĽ���ΪC������AB��AC�����C�����꼰��ABC�������
��3���ڵ�һ�����ڣ�ֱ��д��������������ֵ����ֱ��BC��ֵʱ���Ա���x��ȡֵ��Χ��
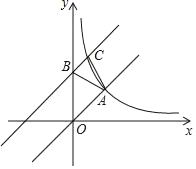
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Ϊ����ѧУ���AB�ĸ߶ȣ�С���������ǰ��6�״��ĵ�C���������¶�Ϊi��1��![]() ��б��CDǰ��2
��б��CDǰ��2![]() �����D���ڵ�D�����ò����DE�������˶���A������Ϊ30�㣬���ò����DE�ĸ�Ϊ1.5�ף�A��B��C��D��E��ͬһƽ���ڣ�����˺Ͳ���Ƕ�����洹ֱ��
�����D���ڵ�D�����ò����DE�������˶���A������Ϊ30�㣬���ò����DE�ĸ�Ϊ1.5�ף�A��B��C��D��E��ͬһƽ���ڣ�����˺Ͳ���Ƕ�����洹ֱ��
(1)���D��Ǧ���߶�(�����������)��
(2)�����AB�ĸ߶�(�����������)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������OABC�Ķ���O������ԭ�㣬A��C�ֱ���x��y����������ϣ�����B��8��6����ֱ��y=-x+b������A��BC��D����y���ڵ�M����P��AD���е㣬ֱ��OP��AB�ڵ�E
��1�����D�����꼰ֱ��OP�Ľ���ʽ��
��2�����ODP�����������ֱ��AD����һ��N��ʹ��AEN��������ڡ�ODP��������������N������
��3����x������һ��T��t��0����5��t��8��������T��x��Ĵ��ߣ��ֱ�ֱ��OE��AD�ڵ�F��G�����߶�AE���Ƿ����һ��Q��ʹ�á�FGQΪ����ֱ�������Σ������ڣ��������Q�����꼰��Ӧ��t��ֵ���������ڣ���˵������.
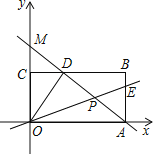
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com