
ЁОЬтФПЁПФГЭјЕъОгЊвЛжжЦЗХЦЫЎЙћЃЌЦфНјМлЮЊ10дЊ/ЧЇПЫЃЌБЃЯЪЦкЮЊ25ЬьЃЌУПЬьЯњЪлСП![]() (ЧЇПЫ)гыЯњЪлЕЅМл
(ЧЇПЫ)гыЯњЪлЕЅМл![]() (дЊ/ЧЇПЫ)жЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪО.
(дЊ/ЧЇПЫ)жЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪО.
(1)Чѓ![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ЕБИУЦЗХЦЫЎЙћЖЈМлЮЊЖрЩйдЊЪБЃЌУПЬьЯњЪлЫљЛёЕУЕФРћШѓзюДѓЃП
(3)ШєИУЭјЕъвЛДЮадЙКНјИУЦЗХЦЫЎЙћ3000ЧЇПЫЃЌИљОн(2)жаУПЬьЛёЕУзюДѓРћШѓЕФЗНЪННјааЯњЪлЃЌЗЂЯждкБЃЯЪЦкФкВЛФмМАЪБЯњЪлЭъБЯЃЌгкЪЧОіЖЈдкБЃЯЪЦкЕФзюКѓ5ЬьвЛДЮадНЕМлЯњЪлЃЌЧѓзюКѓ5ЬьУПЧЇПЫжСЩйНЕМлЖрЩйдЊВХФмШЋВПЪлЭъЃП

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉИУЦЗХЦЫЎЙћЖЈМлЮЊ
ЃЛЃЈ2ЃЉИУЦЗХЦЫЎЙћЖЈМлЮЊ![]() дЊЪБЃЌУПЬьЯњЪлЫљЛёЕУЕФРћШѓзюДѓЃЛЃЈ3ЃЉзюКѓ5ЬьУПЧЇПЫжСЩйНЕМл
дЊЪБЃЌУПЬьЯњЪлЫљЛёЕУЕФРћШѓзюДѓЃЛЃЈ3ЃЉзюКѓ5ЬьУПЧЇПЫжСЩйНЕМл![]() дЊВХФмШЋВПЪлЭъ.
дЊВХФмШЋВПЪлЭъ.
ЁОНтЮіЁП
ЃЈ1ЃЉвРОнЬтвтРћгУД§ЖЈЯЕЪ§ЗЈПЩЕУГіУПЬьЕФЯњЪлСПyЃЈЧЇПЫЃЉгыЯњЪлЕЅМлxЃЈдЊ/ЧЇПЫЃЉжЎМфКЏЪ§ЙиЯЕЃКy=-10x+300ЃЌ
ЃЈ2ЃЉИљОнЯњЪлРћШѓ=ЯњЪлСПЁСЃЈЪлМл-НјМлЃЉЃЌСаГіЦНОљУПЬьЕФЯњЪлРћШѓwЃЈдЊЃЉгыЯњЪлМлxЃЈдЊ/ЧЇПЫЃЉжЎМфЕФКЏЪ§ЙиЯЕЪННјааЧѓНтМДПЩЃЛ
ЃЈ3ЃЉИљОнЬтвтСаГіВЛЕШЪН![]() НјааЧѓНтМДПЩ.
НјааЧѓНтМДПЩ.
ЃЈ1ЃЉЩш![]() ЃЌНЋ
ЃЌНЋ![]() КЭ
КЭ![]() ДњШы
ДњШы![]() ЕУЃК
ЕУЃК
![]()
НтЕУ![]()
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшУПЬьЯњЪлЫљЛёЕУЕФРћШѓЮЊ![]() ,дђ
,дђ
![]()
![]()
![]() ЃЌ
ЃЌ
Ёп0ЃМ![]() Ём25ЃЌЁрЕБ
Ём25ЃЌЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁзюДѓжЕ1000ЃЌ
ШЁзюДѓжЕ1000ЃЌ
Д№ЃКИУЦЗХЦЫЎЙћЖЈМлЮЊ![]() дЊЪБЃЌУПЬьЯњЪлЫљЛёЕУЕФРћШѓзюДѓ.
дЊЪБЃЌУПЬьЯњЪлЫљЛёЕУЕФРћШѓзюДѓ.
ЃЈ3ЃЉНЋ![]() ДњШы
ДњШы![]() ЃЌЕУ
ЃЌЕУ![]() ЃЌЩшзюКѓ5ЬьУПЧЇПЫвЛДЮадНЕМл
ЃЌЩшзюКѓ5ЬьУПЧЇПЫвЛДЮадНЕМл![]() дЊЃЌ
дЊЃЌ
вРЬтвтЕУЃК![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЫљвдзюКѓ5ЬьУПЧЇПЫжСЩйНЕМл![]() дЊВХФмШЋВПЪлЭъ.
дЊВХФмШЋВПЪлЭъ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпЃљЃНЃј![]() ЃЃсЃјЃЋЃс
ЃЃсЃјЃЋЃс![]() Ѓ4ЃсЃ4гыЃјжсЯрНЛгкЕуAКЭЕуBЃЌгыЃљжсЯрНЛгкЕуDЃЈ0ЃЌ8ЃЉЃЌжБЯпDCЦНаагкЃјжсЃЌНЛХзЮяЯпгкСэвЛЕуCЃЌЖЏЕуPвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШДгCЕуГіЗЂЃЌбиCЁњDдЫЖЏЃЌЭЌЪБЃЌЕуQвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуAГіЗЂЃЌбиAЁњBдЫЖЏЃЌСЌНгPQЁЂCBЃЌЩшЕуPдЫЖЏЕФЪБМфЮЊtУыЃЎ
Ѓ4ЃсЃ4гыЃјжсЯрНЛгкЕуAКЭЕуBЃЌгыЃљжсЯрНЛгкЕуDЃЈ0ЃЌ8ЃЉЃЌжБЯпDCЦНаагкЃјжсЃЌНЛХзЮяЯпгкСэвЛЕуCЃЌЖЏЕуPвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШДгCЕуГіЗЂЃЌбиCЁњDдЫЖЏЃЌЭЌЪБЃЌЕуQвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШДгЕуAГіЗЂЃЌбиAЁњBдЫЖЏЃЌСЌНгPQЁЂCBЃЌЩшЕуPдЫЖЏЕФЪБМфЮЊtУыЃЎ
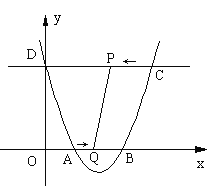
ЃЈЃБЃЉЧѓЃсЕФжЕЃЛЃЈЃВЃЉЕБЫФБпаЮODPQЮЊОиаЮЪБЃЌЧѓетИіОиаЮЕФУцЛ§ЃЛЃЈЃГЃЉЕБЫФБпаЮPQBCЕФУцЛ§ЕШгк14ЪБЃЌЧѓtЕФжЕЃЎЃЈЃДЃЉЕБtЮЊКЮжЕЪБЃЌЁїPBQЪЧЕШбќШ§НЧаЮЃПЃЈжБНгаДГіД№АИЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮКЏЪ§y1ЃНkx+bгыy2ЃНx+aЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлЃКЂйkЃМ0ЃЛЂкaЃО0ЃЛЂлЕБxЃМ3ЪБЃЌy1ЃМy2ЃЛЂмЕБy1ЃО0Чвy2ЃО0ЪБЃЌЉaЃМxЃМ4ЃЎЦфжае§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
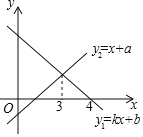
A. 1ИіB. 2ИіC. 3ИіD. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЃЈ4ЃЌ0ЃЉЃЌOЮЊзјБъдЕуЃЌPЪЧЯпЖЮOAЩЯШЮвтвЛЕуЃЈВЛКЌЖЫЕуOЃЌAЃЉЃЌЙ§PЁЂOСНЕуЕФЖўДЮКЏЪ§y1КЭЙ§PЁЂAСНЕуЕФЖўДЮКЏЪ§y2ЕФЭМЯѓПЊПкОљЯђЯТЃЌЫќУЧЕФЖЅЕуЗжБ№ЮЊBЁЂCЃЌЩфЯпOBгыACЯрНЛгкЕуDЃЎЕБOD=AD=3ЪБЃЌетСНИіЖўДЮКЏЪ§ЕФзюДѓжЕжЎКЭЕШгкЃЈ ЃЉ

AЃЎ![]() BЃЎ
BЃЎ![]() CЃЎ3 DЃЎ4
CЃЎ3 DЃЎ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпОЙ§ЕуAЃЈ![]() ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉШ§ЕуЃЌЕуDгыЕуCЙигк
ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉШ§ЕуЃЌЕуDгыЕуCЙигк![]() жсЖдГЦЃЌЕуPЪЧ
жсЖдГЦЃЌЕуPЪЧ![]() жсЩЯЕФвЛИіЖЏЕуЃЌЩшЕуPЕФзјБъЮЊЃЈ
жсЩЯЕФвЛИіЖЏЕуЃЌЩшЕуPЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЃЌЙ§ЕуPзї
ЃЌ0ЃЉЃЌЙ§ЕуPзї![]() жсЕФДЙЯпНЛХзЮяЯпгкЕуQЃЌНЛжБЯпBDгкЕуMЃЎ
жсЕФДЙЯпНЛХзЮяЯпгкЕуQЃЌНЛжБЯпBDгкЕуMЃЎ
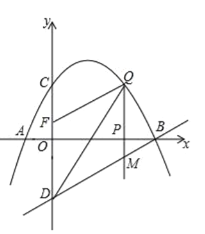
ЃЈ1ЃЉЧѓИУХзЮяЯпЫљБэЪОЕФЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕуPдкЯпЖЮABЩЯдЫЖЏЕФЙ§ГЬжаЃЌЪЧЗёДцдкЕуQЃЌЪЙЕУвдBЁЂQЁЂMЮЊЖЅЕуЕФШ§НЧаЮгыЁїBODЯрЫЦЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉвбжЊЕуFЃЈ0ЃЌ![]() ЃЉЃЌЕуPдк
ЃЉЃЌЕуPдк![]() жсЩЯдЫЖЏЃЌЪдЧѓЕБ
жсЩЯдЫЖЏЃЌЪдЧѓЕБ![]() ЮЊКЮжЕЪБЃЌвдDЁЂMЁЂQЁЂFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЎ
ЮЊКЮжЕЪБЃЌвдDЁЂMЁЂQЁЂFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃН6ЃЌBCЃН![]() ЃЌЕуEДгAГіЗЂбиЯпЖЮACдЫЖЏжСЕуCЭЃжЙЃЌEDЁЭABЃЌEFЁЭACЃЌНЋЁїADEбижБЯпEFЗелЕУЕНЁїAЁфDЁфEЃЌЩшDEЃНxЃЌЁїAЁфDЁфEгыЁїABCжиКЯВПЗжЕФУцЛ§ЮЊyЃЎ
ЃЌЕуEДгAГіЗЂбиЯпЖЮACдЫЖЏжСЕуCЭЃжЙЃЌEDЁЭABЃЌEFЁЭACЃЌНЋЁїADEбижБЯпEFЗелЕУЕНЁїAЁфDЁфEЃЌЩшDEЃНxЃЌЁїAЁфDЁфEгыЁїABCжиКЯВПЗжЕФУцЛ§ЮЊyЃЎ
ЃЈ1ЃЉЕБxЃНЁЁ ЁЁЪБЃЌDЁфЧЁКУТфдкBCЩЯЃП
ЃЈ2ЃЉЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіxЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
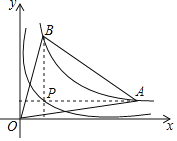
ЁОЬтФПЁПШчЭМЃЌЕуPЮЊКЏЪ§yЃН![]() ЃЈxЃО0ЃЉЭМЯѓЩЯвЛЕуЃЌЙ§ЕуPзїxжсЁЂyжсЕФЦНааЯпЃЌЗжБ№гыКЏЪ§yЃН
ЃЈxЃО0ЃЉЭМЯѓЩЯвЛЕуЃЌЙ§ЕуPзїxжсЁЂyжсЕФЦНааЯпЃЌЗжБ№гыКЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкЕуAЁЂBЃЌдђЁїAOBЕФУцЛ§ЮЊ_____ЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкЕуAЁЂBЃЌдђЁїAOBЕФУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
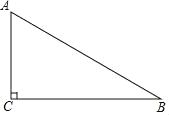
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЎ
ЃЈ1ЃЉгУГпЙцдкБпBCЩЯЧѓзївЛЕуPЃЌЪЙPAЃНPBЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉЃЛ
ЃЈ2ЃЉСЌНгAPЃЌШєAPЦНЗжЁЯCABЃЌЧѓЁЯBЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
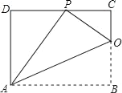
ЁОЬтФПЁПвбжЊОиаЮABCDЕФвЛЬѕБпADЃН8ЃЌНЋОиаЮABCDелЕўЃЌЪЙЕУЖЅЕуBТфдкCDБпЩЯЕФPЕуДІЃЎШчЭМЃЌвбжЊелКлгыБпBCНЛгкЕуOЃЌСЌНсAPЁЂOPЁЂOAЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїOCPЁзЁїPDAЃЛ
ЃЈ2ЃЉШєtanЁЯPAOЃН![]() ЃЌЧѓБпABЕФГЄЃЎ
ЃЌЧѓБпABЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com