
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于点O,连结AP、OP、OA.
(1)求证:△OCP∽△PDA;
(2)若tan∠PAO=![]() ,求边AB的长.
,求边AB的长.
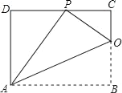
【答案】(1)见解析;(2)AB=10.
【解析】
(1)只需要证明两对对应角分别相等即可证明相似(2)根据题①可知CP=4,设BO=x,则CO=8﹣x,PD=2(8﹣x),即可解答
(1)证明:∵四边形ABCD为矩形,
∴∠B=∠C=∠D=90°.
由折叠,可知:∠APO=∠B=90°,
∴∠APD+∠CPO=90°.
∵∠APD+∠DAP=90°,
∴∠DAP=∠CPO,
∴△OCP∽△PDA;
(2)解:由折叠,可知:∠APO=∠B=90°,AP=AB,PO=BO,tan∠PAO=![]() =
=![]() =
=![]() .
.
∵△OCP∽△PDA,
∴![]()
∵AD=8,
∴CP=4.
设BO=x,则CO=8﹣x,PD=2(8﹣x),
∴AB=2x=CD=PD+CP=2(8﹣x)+4,
解得:x=5,
∴AB=10.



科目:初中数学 来源: 题型:
【题目】某网店经营一种品牌水果,其进价为10元/千克,保鲜期为25天,每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)之间的函数关系如图所示.
(元/千克)之间的函数关系如图所示.
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)当该品牌水果定价为多少元时,每天销售所获得的利润最大?
(3)若该网店一次性购进该品牌水果3000千克,根据(2)中每天获得最大利润的方式进行销售,发现在保鲜期内不能及时销售完毕,于是决定在保鲜期的最后5天一次性降价销售,求最后5天每千克至少降价多少元才能全部售完?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
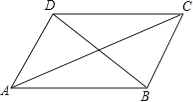
A.①②B.②③C.①③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为二次函数y=ax2+bx+c的图象,则下列说法中错误的是( )
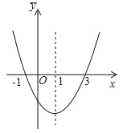
A. abc>0B. 2a+b=1
C. 4a+2b+c<0D. 对于任意x均有ax2+bx≥a+b
查看答案和解析>>
科目:初中数学 来源: 题型:
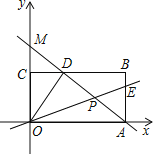
【题目】如图,已知长方形OABC的顶点O在坐标原点,A、C分别在x、y轴的正半轴上,顶点B(8,6),直线y=-x+b经过点A交BC于D、交y轴于点M,点P是AD的中点,直线OP交AB于点E
(1)求点D的坐标及直线OP的解析式;
(2)求△ODP的面积,并在直线AD上找一点N,使△AEN的面积等于△ODP的面积,请求出点N的坐标
(3)在x轴上有一点T(t,0)(5<t<8),过点T作x轴的垂线,分别交直线OE、AD于点F、G,在线段AE上是否存在一点Q,使得△FGQ为等腰直角三角形,若存在,请求出点Q的坐标及相应的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是_____.
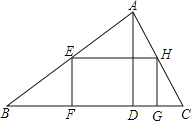
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 上部分点的横坐标
上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
![]()
小聪观察上表,得出下面结论:①抛物线与x轴的一个交点为(3,0); ②函数![]() 的最大值为6;③抛物线的对称轴是
的最大值为6;③抛物线的对称轴是![]() ;④在对称轴左侧,y随x增大而增大.其中正确有( )
;④在对称轴左侧,y随x增大而增大.其中正确有( )
A. ①②B. ①③C. ①②③D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD,AC是∠BAD的角平分线.
(1)求证:△ABC≌△ADC.
(2)若∠BCD=60°,AC=BC,求∠ADB的度数.
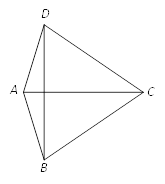
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com