
ЁОЬтФПЁПФГЕїВщЛњЙЙНЋНёФъЛЦЪЏЪаУёзюЙизЂЕФШШЕуЛАЬтЗжЮЊЯћЗбЁЂНЬг§ЁЂЛЗБЃЁЂЗДИЏМАЦфЫќЙВЮхРрЃЎИљОнзюНќвЛДЮЫцЛњЕїВщЕФЯрЙиЪ§ОнЃЌЛцжЦЕФЭГМЦЭМБэШчЯТЃК
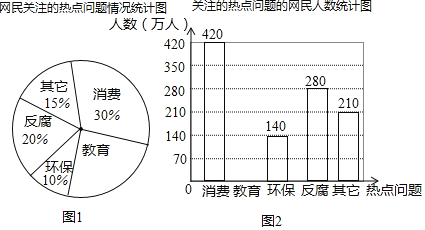
ИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮЙВЕїВщ ШЫЃЌЧыдкЭМЩЯВЙШЋЬѕаЮЭГМЦЭМВЂБъГіЯргІЪ§ОнЃЛ
ЃЈ2ЃЉШєЛЦЪЏЪадМга260ЭђШЫПкЃЌЧыФуЙРМЦзюЙизЂНЬг§ЮЪЬтЕФШЫЪ§дМЮЊЖрЩйЭђШЫЃП
ЃЈ3ЃЉЫцзХОМУЕФЗЂеЙЃЌШЫУЧдНРДдНжиЪгНЬг§ЃЌдЄМЦЙизЂНЬг§ЕФШЫЪ§дкУПФъвд10ЃЅЕФдіГЄТЪдкдіГЄЃЌдЄМЦСНФъКѓЮвЪаЙизЂНЬг§ЮЪЬтЕФШЫЪ§.
ЁОД№АИЁПЃЈ1ЃЉ1400ЃЌМћНтЮіЃЛЃЈ2ЃЉ65ЃЛЃЈ3ЃЉ78.65Эђ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЙизЂЯћЗбЕФШЫЪ§ЪЧ420ШЫЃЌЫљеМЕФБШР§ЪНЪЧ30%ЃЌМДПЩЧѓЕУзмШЫЪ§ЃЌШЛКѓРћгУзмШЫЪ§ГЫвдЙизЂНЬг§ЕФБШР§ЧѓЕУЙизЂНЬг§ЕФШЫЪ§ЃЌНјЖјПЩВЙШЋЬѕаЮЭГМЦЭМВЂБъГіЯргІЪ§ОнЃЛ
ЃЈ2ЃЉРћгУзмШЫЪ§ГЫвдЖдгІЕФАйЗжБШМДПЩЃЛ
ЃЈ3ЃЉРћгУЃЈ2ЃЉжаЕФНЬг§ШЫЪ§ГЫвдЃЈ1+10ЃЅЃЉ2МДПЩЕУЕННсЙћ.
НтЃКЃЈ1ЃЉЕїВщЕФзмШЫЪ§ЪЧЃК420ЁТ30%=1400ЃЈШЫЃЉЃЌ
ЙизЂНЬг§ЕФШЫЪ§ЪЧЃК1400ЁС25%=350ЃЈШЫЃЉЃЎ
 ЃЛ
ЃЛ
ЃЈ2ЃЉ![]() ЃЈЭђЃЉ
ЃЈЭђЃЉ
ЃЈ3ЃЉ65ЁСЃЈ1+10ЃЅЃЉ2=78.65ЃЈЭђЃЉ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКе§ЗНаЮABCDЃЌЕШбќжБНЧШ§НЧАхЕФжБНЧЖЅЕуТфдке§ЗНаЮЕФЖЅЕуDДІЃЌЪЙШ§НЧАхШЦЕуDа§зЊЃЎ

ЃЈ1ЃЉЕБШ§НЧАха§зЊЕНЭМ1ЕФЮЛжУЪБЃЌВТЯыCEгыAFЕФЪ§СПЙиЯЕЃЌВЂМгвджЄУїЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШєDEЃКAEЃКCEЃН1ЃК![]() ЃК3ЃЌЧѓЁЯAEDЕФЖШЪ§ЃЛ
ЃК3ЃЌЧѓЁЯAEDЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШєBCЃН4ЃЌЕуMЪЧБпABЕФжаЕуЃЌСЌНсDMЃЌDMгыACНЛгкЕуOЃЌЕБШ§НЧАхЕФБпDFгыБпDMжиКЯЪБЃЈШчЭМ2ЃЉЃЌШєOFЃН![]() ЃЌЧѓDFКЭDNЕФГЄЃЎ
ЃЌЧѓDFКЭDNЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаХаЖЯе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. МзввСНзщбЇЩњЩэИпЕФЦНОљЪ§ОљЮЊ1.58ЃЌЗНВюЗжБ№ЮЊSМз2ЃН2.3ЃЌSвв2ЃН1.8ЃЌдђМззщбЇЩњЕФЩэИпНЯећЦы
B. ЮЊСЫСЫНтФГЯиЦпФъМЖ4000УћбЇЩњЕФЦкжаЪ§бЇГЩМЈЃЌДгжаГщШЁ100УћбЇЩњЕФЪ§бЇГЩМЈНјааЕїВщЃЌетИіЮЪЬтжабљБОШнСПЮЊ4000
C. дкЁАЭЏаФЯђЕГЃЌбєЙтЯТГЩГЄЁБКЯГЊБШШќжаЃЌ30ИіВЮШќЖгЕФОіШќГЩМЈШчЯТБэЃКдђет30ИіВЮШќЖгОіШќГЩМЈЕФжаЮЛЪ§ЪЧ9.7

D. га13УћЭЌбЇГіЩњгк2003ФъЃЌФЧУДдкетИіЮЪЬтжаЁАжСЩйгаСНУћЭЌбЇГіЩњдкЭЌвЛИідТЁБЪєгкБиШЛЪТМў
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛДЮКЏЪ§y1ЃНkx+bгыy2ЃНx+aЕФЭМЯѓШчЭМЫљЪОЃЌдђЯТСаНсТлЃКЂйkЃМ0ЃЛЂкaЃО0ЃЛЂлЕБxЃМ3ЪБЃЌy1ЃМy2ЃЛЂмЕБy1ЃО0Чвy2ЃО0ЪБЃЌЉaЃМxЃМ4ЃЎЦфжае§ШЗЕФИіЪ§ЪЧЃЈЁЁЁЁЃЉ
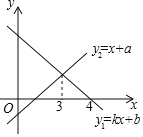
A. 1ИіB. 2ИіC. 3ИіD. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCКЭЁїADEжаЃЌBAЃНBCЃЌDAЃНDEЃЌЧвЁЯABCЃНЁЯADEЃЌЕуEдкЁїABCЕФФкВПЃЌСЌНгECЃЌEBКЭEDЃЌЩшECЃНkBDЃЈkЁй0ЃЉЃЎ
ЃЈ1ЃЉЕБЁЯABCЃНЁЯADEЃН60ЁуЪБЃЌШчЭМ1ЃЌЧыЧѓГіkжЕЃЌВЂИјгшжЄУїЃЛ
ЃЈ2ЃЉЕБЁЯABCЃНЁЯADEЃН90ЁуЪБЃК
ЂйШчЭМ2ЃЌЃЈ1ЃЉжаЕФkжЕЪЧЗёЗЂЩњБфЛЏЃЌШчЮоБфЛЏЃЌЧыИјгшжЄУїЃЛШчгаБфЛЏЃЌЧыЧѓГіkжЕВЂЫЕУїРэгЩЃЛ
ЂкШчЭМ3ЃЌЕБDЃЌEЃЌCШ§ЕуЙВЯпЃЌЧвEЮЊDCжаЕуЪБЃЌЧыЧѓГіtanЁЯEACЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуAЃЈ4ЃЌ0ЃЉЃЌOЮЊзјБъдЕуЃЌPЪЧЯпЖЮOAЩЯШЮвтвЛЕуЃЈВЛКЌЖЫЕуOЃЌAЃЉЃЌЙ§PЁЂOСНЕуЕФЖўДЮКЏЪ§y1КЭЙ§PЁЂAСНЕуЕФЖўДЮКЏЪ§y2ЕФЭМЯѓПЊПкОљЯђЯТЃЌЫќУЧЕФЖЅЕуЗжБ№ЮЊBЁЂCЃЌЩфЯпOBгыACЯрНЛгкЕуDЃЎЕБOD=AD=3ЪБЃЌетСНИіЖўДЮКЏЪ§ЕФзюДѓжЕжЎКЭЕШгкЃЈ ЃЉ

AЃЎ![]() BЃЎ
BЃЎ![]() CЃЎ3 DЃЎ4
CЃЎ3 DЃЎ4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпОЙ§ЕуAЃЈ![]() ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉШ§ЕуЃЌЕуDгыЕуCЙигк
ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉШ§ЕуЃЌЕуDгыЕуCЙигк![]() жсЖдГЦЃЌЕуPЪЧ
жсЖдГЦЃЌЕуPЪЧ![]() жсЩЯЕФвЛИіЖЏЕуЃЌЩшЕуPЕФзјБъЮЊЃЈ
жсЩЯЕФвЛИіЖЏЕуЃЌЩшЕуPЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЃЌЙ§ЕуPзї
ЃЌ0ЃЉЃЌЙ§ЕуPзї![]() жсЕФДЙЯпНЛХзЮяЯпгкЕуQЃЌНЛжБЯпBDгкЕуMЃЎ
жсЕФДЙЯпНЛХзЮяЯпгкЕуQЃЌНЛжБЯпBDгкЕуMЃЎ
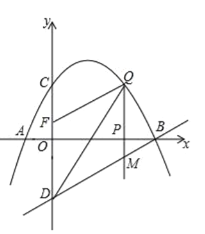
ЃЈ1ЃЉЧѓИУХзЮяЯпЫљБэЪОЕФЖўДЮКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉЕуPдкЯпЖЮABЩЯдЫЖЏЕФЙ§ГЬжаЃЌЪЧЗёДцдкЕуQЃЌЪЙЕУвдBЁЂQЁЂMЮЊЖЅЕуЕФШ§НЧаЮгыЁїBODЯрЫЦЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉвбжЊЕуFЃЈ0ЃЌ![]() ЃЉЃЌЕуPдк
ЃЉЃЌЕуPдк![]() жсЩЯдЫЖЏЃЌЪдЧѓЕБ
жсЩЯдЫЖЏЃЌЪдЧѓЕБ![]() ЮЊКЮжЕЪБЃЌвдDЁЂMЁЂQЁЂFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЎ
ЮЊКЮжЕЪБЃЌвдDЁЂMЁЂQЁЂFЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
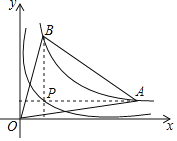
ЁОЬтФПЁПШчЭМЃЌЕуPЮЊКЏЪ§yЃН![]() ЃЈxЃО0ЃЉЭМЯѓЩЯвЛЕуЃЌЙ§ЕуPзїxжсЁЂyжсЕФЦНааЯпЃЌЗжБ№гыКЏЪ§yЃН
ЃЈxЃО0ЃЉЭМЯѓЩЯвЛЕуЃЌЙ§ЕуPзїxжсЁЂyжсЕФЦНааЯпЃЌЗжБ№гыКЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкЕуAЁЂBЃЌдђЁїAOBЕФУцЛ§ЮЊ_____ЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкЕуAЁЂBЃЌдђЁїAOBЕФУцЛ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїМввћЫЎЛњжадгаЫЎЕФЮТЖШЮЊ20ЁцЃЌЭЈЕчПЊЛњКѓЃЌвћЫЎЛњздЖЏПЊЪММгШШ[ДЫЙ§ГЬжаЫЎЮТyЃЈЁцЃЉгыПЊЛњЪБМфxЃЈЗжЃЉТњзувЛДЮКЏЪ§ЙиЯЕ]ЃЌЕБМгШШЕН100ЁцЪБздЖЏЭЃжЙМгШШЃЌЫцКѓЫЎЮТПЊЪМЯТНЕ[ДЫЙ§ГЬжаЫЎЮТyЃЈЁцЃЉгыПЊЛњЪБМфxЃЈЗжЃЉГЩЗДБШР§ЙиЯЕ]ЃЌЕБЫЎЮТНЕжС20ЁцЪБЃЌвћЫЎЛњгжздЖЏПЊЪММгШШЁЃЌжиИДЩЯЪіГЬађЃЈШчЭМЫљЪОЃЉЃЌИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЕБ0ЁмxЁм8ЪБЃЌЧѓЫЎЮТyЃЈЁцЃЉгыПЊЛњЪБМфxЃЈЗжЃЉЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓЭМжаtЕФжЕЃЛ
ЃЈ3ЃЉШєаЁУїдкЭЈЕчПЊЛњКѓМДЭтГіЩЂВНЃЌЧыФудЄВтаЁУїЩЂВН45ЗжжгЛиЕНМвЪБЃЌвћЫЎЛњФкЕФЮТЖШдМЮЊЖрЩйЁцЃП

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com