
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬өгOОӘЧшұкФӯөгЈ¬ЦұПЯy=©Ғx+nУлxЦбЎўyЦб·ЦұрҪ»УЪBЎўCБҪөгЈ¬ЕЧОпПЯy=ax2+bx+3(aЎЩ0)№эCЎўBБҪөгЈ¬Ҫ»xЦбУЪБнТ»өгAЈ¬Б¬ҪУACЈ¬ЗТtanЎПCAO=3Ј®
(1)ЗуЕЧОпПЯөДҪвОцКҪЈ»
(2)ИфөгPКЗЙдПЯCBЙПТ»өгЈ¬№эөгPЧчxЦбөДҙ№ПЯЈ¬ҙ№ЧгОӘHЈ¬Ҫ»ЕЧОпПЯУЪQЈ¬ЙиPөгәбЧшұкОӘtЈ¬ПЯ¶ОPQөДіӨОӘdЈ¬ЗуіцdУлtЦ®јдөДәҜКэ№ШПөКҪЈ¬ІўРҙіцПаУҰөДЧФұдБҝtөДИЎЦө·¶О§Ј»
(3)ФЪ(2)өДМхјюПВЈ¬өұөгPФЪПЯ¶ОBCЙПКұЈ¬ЙиPH=eЈ¬ТСЦӘdЈ¬eКЗТФyОӘОҙЦӘКэөДТ»ФӘ¶юҙО·ҪіМЈәy2Јӯ(m+3)y+ (5m2Јӯ2m+13)=0 (mОӘіЈКэ)өДБҪёцКөКэёщЈ¬өгMФЪЕЧОпПЯЙПЈ¬Б¬ҪУMQЎўMHЎўPMЈ¬ЗТЈ®MPЖҪ·ЦЎПQMHЈ¬ЗуіцtЦөј°өгMөДЧшұкЈ®
(5m2Јӯ2m+13)=0 (mОӘіЈКэ)өДБҪёцКөКэёщЈ¬өгMФЪЕЧОпПЯЙПЈ¬Б¬ҪУMQЎўMHЎўPMЈ¬ЗТЈ®MPЖҪ·ЦЎПQMHЈ¬ЗуіцtЦөј°өгMөДЧшұкЈ®

(1) y=-x2+2x+3Ј»(2)  Ј»ЈЁ3Ј©t=1, (1+
Ј»ЈЁ3Ј©t=1, (1+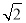 Ј¬2)әН(1Јӯ
Ј¬2)әН(1Јӯ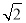 Ј¬2).
Ј¬2).
ЎҫҪвОцЎҝ
КФМв·ЦОцЈәЈЁ1Ј©өұx=0КұҙъИлЕЧОпПЯy=ax2+bx+3ЈЁaЎЩ0Ј©ҫНҝЙТФЗуіцy=3¶шөГіцCөДЧшұкЈ¬ҫНҝЙТФөГіцЦұПЯөДҪвОцКҪЈ¬ҫНҝЙТФЗуіцBөДЧшұкЈ¬ФЪЦұҪЗИэҪЗРОAOCЦРЈ¬УЙИэҪЗРОәҜКэЦөҫНҝЙТФЗуіцOAөДЦөЈ¬өГіцAөДЧшұкЈ¬ФЩУЙҙэ¶ЁПөКэ·ЁҪЁБў¶юФӘТ»ҙО·ҪіМЧйЗуіцЖдҪвҫНҝЙТФөГіцҪбВЫЈ»
ЈЁ2Ј©·ЦБҪЦЦЗйҝцМЦВЫЈ¬өұөгPФЪПЯ¶ОCBЙПКұЈ¬әНИзНј3өгPФЪЙдПЯBNЙПКұЈ¬ҫНУРPөгөДЧшұкОӘЈЁtЈ¬-t+3Ј©Ј¬QөгөДЧшұкОӘЈЁtЈ¬-t2+2t+3Ј©Ј¬ҫНҝЙТФөГіцdУлtЦ®јдөДәҜКэ№ШПөКҪ¶шөГіцҪбВЫЈ»
ЈЁ3Ј©ёщҫЭёщөДЕРұрКҪҫНҝЙТФЗуіцmөДЦөЈ¬ҫНҝЙТФЗуіц·ҪіМөДҪв¶шЗуөГPQәНPHөДЦөЈ¬СУіӨMPЦБLЈ¬К№LP=MPЈ¬Б¬ҪУLQЎўLHЈ¬ИзНј2Ј¬СУіӨMPЦБLЈ¬К№LP=MPЈ¬Б¬ҪУLQЎўLHЈ¬ҫНҝЙТФөГіцЛДұЯРОLQMHКЗЖҪРРЛДұЯРОЈ¬Ҫш¶шөГіцЛДұЯРОLQMHКЗБвРОЈ¬УЙБвРОөДРФЦКҫНҝЙТФЗуіцҪбВЫЈ®
КФМвҪвОцЈәЈЁ1Ј©өұx=0Ј¬Фтy=-x+n=0+n=nЈ¬y=ax2+bx+3=3Ј¬
ЎаOC=3=nЈ®
өұy=0Ј¬
Ўа-x+3=0Ј¬x=3=OBЈ¬
ЎаBЈЁ3Ј¬0Ј©Ј®
ФЪЎчAOCЦРЈ¬ЎПAOCЈҪ90ЎгЈ¬tanЎПCAO=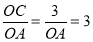 Ј¬
Ј¬
ЎаOA=1Ј¬
ЎаAЈЁ-1Ј¬0Ј©Ј®
Ҫ«AЈЁ-1Ј¬0Ј©Ј¬BЈЁ3Ј¬0Ј©ҙъИлy=ax2+bx+3Ј¬
өГ
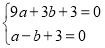 Ј¬
Ј¬
ҪвөГЈә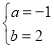
ЎаЕЧОпПЯөДҪвОцКҪЈәy=-x2+2x+3Ј»
(2) ИзНј1Ј¬

ЎЯPөгөДәбЧшұкОӘt ЗТPQҙ№ЦұУЪxЦб ЎаPөгөДЧшұкОӘ(tЈ¬Јӯt+3)Ј¬
QөгөДЧшұкОӘ(tЈ¬Јӯt2+2t+3).
ЎаPQ=|(Јӯt+3)Јӯ(Јӯt2+2t+3)|=| t2Јӯ3t |
Ўа Ј»
Ј»
ЎЯdЈ¬eКЗy2Јӯ(m+3)y+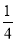 (5m2Јӯ2m+13)=0ЈЁmОӘіЈКэЈ©өДБҪёцКөКэёщЈ¬
(5m2Јӯ2m+13)=0ЈЁmОӘіЈКэЈ©өДБҪёцКөКэёщЈ¬
ЎаЎчЎЭ0Ј¬јҙЎч=(m+3)2Јӯ4ЎБ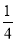 (5m2Јӯ2m+13)ЎЭ0
(5m2Јӯ2m+13)ЎЭ0
ХыАнөГЈәЎч= Јӯ4(mЈӯ1)2ЎЭ0Ј¬ЎЯЈӯ4(mЈӯ1)2ЎЬ0Ј¬
ЎаЎч=0Ј¬m=1Ј¬
Ўа PQУлPHКЗy2Јӯ4y+4=0өДБҪёцКөКэёщЈ¬ҪвөГ y1=y2=2
y1=y2=2
Ўа PQ=PH=2Ј¬ ЎаЈӯt+3=2Ј¬Ўаt=1,
ЎаҙЛКұQКЗЕЧОпПЯөД¶ҘөгЈ¬
СУіӨMPЦБLЈ¬К№LP=MPЈ¬Б¬ҪУLQЎўLHЈ¬ИзНј2Ј¬

ЎЯLP=MPЈ¬PQ=PHЈ¬ЎаЛДұЯРОLQMHКЗЖҪРРЛДұЯРОЈ¬
ЎаLHЎОQMЈ¬ЎаЎП1=ЎП3Ј¬ЎЯЎП1=ЎП2Ј¬ЎаЎП2=ЎП3Ј¬
ЎаLH=MHЈ¬ЎаЖҪРРЛДұЯРОLQMHКЗБвРОЈ¬
ЎаPMЎНQHЈ¬ЎаөгMөДЧЭЧшұкУлPөгЧЭЧшұкПаН¬Ј¬¶јКЗ2Ј¬
ЎаФЪy=Јӯx2+2x+3Боy=2Ј¬өГx2Јӯ2xЈӯ1=0Ј¬Ўаx1=1+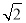 Ј¬x2=1Јӯ
Ј¬x2=1Јӯ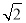
ЧЫЙПЈәtЦөОӘ1Ј¬MөгЧшұкОӘ(1+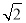 Ј¬2)әН(1Јӯ
Ј¬2)әН(1Јӯ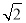 Ј¬2)
Ј¬2)
ҝјөгЈә¶юҙОәҜКэЧЫәПМвЈ®


 МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё
МмМмПтЙПТ»ұҫәГҫнПөБРҙр°ё РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
РЎС§Йъ10·ЦЦУУҰУГМвПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2013-2014С§ДкҪӯЛХКЎОЮОэКРіз°ІЗшҫЕДкј¶ПВС§ЖЪЖЪЦРНіҝјЈЁТ»ДЈЈ©КэС§КФҫнЈЁҪвОц°жЈ© МвРНЈәМоҝХМв
ТСЦӘЙИРОөД°лҫ¶ОӘ4cmЈ¬ФІРДҪЗОӘ120ºЈ¬ФтҙЛЙИРОөД»ЎіӨКЗ .
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2013-2014С§ДкҪӯЛХКЎОЮОэКРТЛРЛНв№ъУпѧУҫЕДкј¶ПВС§ЖЪЖЪЦРҝјКФКэС§КФҫнЈЁҪвОц°жЈ© МвРНЈәСЎФсМв
ПВБРФЛЛгХэИ·өДКЗЈЁЎЎЎЎЈ©
AЈ®a2•a3=a6 BЈ®ЈЁa4Ј©3=a12
CЈ®ЈЁ©Ғ2aЈ©3=©Ғ6a3 DЈ®aЈЁa©Ғ1Ј©=a2©Ғ1
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2013-2014С§ДкҪӯЛХКЎОЮОэКРҫЕДкј¶3ФВҪЧ¶ОІвКФКэС§КФҫнЈЁҪвОц°жЈ© МвРНЈәМоҝХМв
ТтКҪ·ЦЎҫҪвОцЎҝ = Ј®
= Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2013-2014С§ДкҪӯЛХКЎОЮОэКРҫЕДкј¶3ФВҪЧ¶ОІвКФКэС§КФҫнЈЁҪвОц°жЈ© МвРНЈәСЎФсМв
ТСЦӘЎСO1әНЎСO2өД°лҫ¶·ЦұрОӘ2cmәН3cmЈ¬БҪФІөДФІРДҫаОӘ5cmЈ¬ФтБҪФІөДО»ЦГ№ШПөКЗЈЁ Ј©
AЈ®НвЗР BЈ®НвАл CЈ®ПаҪ» DЈ®ДЪЗР
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2013-2014С§ДкҪӯЛХКЎСпЦЭКРЪхҪӯЗшҫЕДкј¶ЦРҝјТ»ДЈКэС§КФҫнЈЁҪвОц°жЈ© МвРНЈәҪвҙрМв
јЧЎўТТЎўұыЎў¶ЎЛДО»Н¬С§ҪшРРТ»ҙОУрГ«ЗтөҘҙтұИИьЈ¬ТӘҙУЦРСЎіцБҪО»Н¬С§ҙтөЪТ»іЎұИИьЈ®
ЈЁ1Ј©ЗлУГКчЧҙНј·Ё»тБРұн·ЁЈ¬ЗуЗЎәГСЎЦРјЧЎўТТБҪО»Н¬С§өДёЕВКЈ»
ЈЁ2Ј©ИфТСИ·¶ЁјЧҙтөЪТ»іЎЈ¬ФЩҙУЖдУаИэО»Н¬С§ЦРЛж»ъСЎИЎТ»О»Ј¬ЗуЗЎәГСЎЦРТТН¬С§өДёЕВКЎЈ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2013-2014С§ДкҪӯЛХКЎСпЦЭКРЪхҪӯЗшҫЕДкј¶ЦРҝјТ»ДЈКэС§КФҫнЈЁҪвОц°жЈ© МвРНЈәМоҝХМв
ИзНјЈ¬ФЪЖҪГжЦұҪЗЧшұкПөЦРЈ¬ ИфЎчABCУлЎчA1B1C1№ШУЪEөгіЙЦРРД¶ФіЖЈ¬ Фт¶ФіЖЦРРДEөгөДЧшұкКЗ Ј®

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2013-2014С§ДкҪӯЛХКЎХЕјТёЫКРҫЕДкј¶5ФВНшЙПФДҫнККУҰРФҝјКФКэС§КФҫнЈЁҪвОц°жЈ© МвРНЈәҪвҙрМв
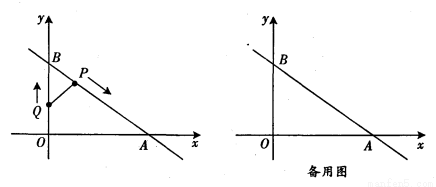
ФЪЖҪГжЦұҪЗЧшұкПөxOyЦРЈ¬Т»ҙОәҜКэyЈҪЈӯ xЈ«3өДНјПуУлxЦбҪ»УЪөгAЈ¬УлyЦбҪ»УЪөгBЈ¬¶ҜөгPҙУөгBіц·ўСШBAПтЦХөгAФЛ¶ҜЈ¬Н¬Кұ¶ҜөгQҙУөгOіц·ўСШOBПтөгBФЛ¶ҜЈ¬өҪҙпөгBәуБўҝМТФФӯАҙөДЛЩ¶ИСШBO·ө»ШЈ®өгPЈ¬QФЛ¶ҜЛЩ¶ИҫщОӘГҝГл1ёцөҘО»іӨ¶ИЈ¬өұөгPөҪҙпөгAКұНЈЦ№ФЛ¶ҜЈ¬өгQТІН¬КұНЈЦ№Ј®Б¬ҪбPQЈ¬ЙиФЛ¶ҜКұјдОӘt(t>0)ГлЈ®
xЈ«3өДНјПуУлxЦбҪ»УЪөгAЈ¬УлyЦбҪ»УЪөгBЈ¬¶ҜөгPҙУөгBіц·ўСШBAПтЦХөгAФЛ¶ҜЈ¬Н¬Кұ¶ҜөгQҙУөгOіц·ўСШOBПтөгBФЛ¶ҜЈ¬өҪҙпөгBәуБўҝМТФФӯАҙөДЛЩ¶ИСШBO·ө»ШЈ®өгPЈ¬QФЛ¶ҜЛЩ¶ИҫщОӘГҝГл1ёцөҘО»іӨ¶ИЈ¬өұөгPөҪҙпөгAКұНЈЦ№ФЛ¶ҜЈ¬өгQТІН¬КұНЈЦ№Ј®Б¬ҪбPQЈ¬ЙиФЛ¶ҜКұјдОӘt(t>0)ГлЈ®
(1)ЗуөгPөДЧшұкЈЁУГә¬tөДҙъКэКҪұнКҫЈ©Ј»
(2)өұөгQҙУөгOПтөгBФЛ¶ҜКұ(ОҙөҪҙпөгB)Ј¬КЗ·сҙжФЪКөКэtЈ¬К№өГЎчBPQөДГж»эҙуУЪ17ИфҙжФЪЈ¬ЗлЗуіцtөДИЎЦө·¶О§Ј»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ»
(3)°йЛжЧЕPЈ¬QБҪөгөДФЛ¶ҜЈ¬ПЯ¶ОPQөДҙ№ЦұЖҪ·ЦПЯОӘЦұПЯlЈ®КЗ·сҙжФЪtөДЦөЈ¬К№өГЦұПЯlҫӯ№эөгO?ИфҙжФЪЈ¬ЗлЗуіцЛщУРtөДЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә2013-2014С§ДкҪӯЛХКЎіЈЦЭКРҫЕДкј¶ЦРҝјТ»ДЈКэС§КФҫнЈЁҪвОц°жЈ© МвРНЈәМоҝХМв
јЖЛгЈә ЈҪ Ј¬
ЈҪ Ј¬ ЈҪ Ј¬
ЈҪ Ј¬ ЈҪ Ј¬
ЈҪ Ј¬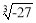 ЈҪ Ј®
ЈҪ Ј®
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com