
分析 (1)分别将$\sqrt{10}$、$\root{3}{25}$与3比较大小即可;
(2)利用作差法将$\frac{\sqrt{5}-1}{2}$-$\frac{1}{2}$得$\frac{\sqrt{5}-2}{2}$,比较$\sqrt{5}$与2的大小即可知.
解答 解:∵$\sqrt{10}$>$\sqrt{9}$,即$\sqrt{10}$>3,
$\root{3}{25}$<$\root{3}{27}$,即$\root{3}{25}$<3,
∴$\sqrt{10}$>$\root{3}{25}$;
(2)$\frac{\sqrt{5}-1}{2}-\frac{1}{2}$=$\frac{\sqrt{5}-2}{2}$,
∵$\sqrt{5}$>$\sqrt{4}$,即$\sqrt{5}$>2,
∴$\frac{\sqrt{5}-2}{2}$>0,
∴$\frac{\sqrt{5}-1}{2}$>$\frac{1}{2}$.
故答案为:>,>.
点评 本题主要考查实数的大小比较,选取合适比较法是比较大小的关键,通常使用作差法、平方法或统一根指数等.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在公园调查了1000名老年人的健康状况 | |
| B. | 调查了10名老年人的健康状况 | |
| C. | 在医院调查了1000名老年人的健康状况 | |
| D. | 利用派出所的户籍网随机调查了该地区10%的老年人健康状况 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
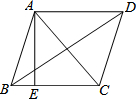 已知菱形ABCD的两条对角线AC,BD长分别为6cm、8cm,且AE⊥BC,这个菱形的面积S=24cm2,AE=$\frac{24}{5}$cm.
已知菱形ABCD的两条对角线AC,BD长分别为6cm、8cm,且AE⊥BC,这个菱形的面积S=24cm2,AE=$\frac{24}{5}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com