
 如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.分析 (1)证明△OMP≌△ONP,即可证得MN⊥OT,且OT平分MN;
(2)①若经过A,B,C,D四个点的圆存在,则对角互补,据此即可判断;
②已知FM⊥AB,作EG⊥AB于G,根据菱形的面积公式求得GE的长,然后根据△BNE∽△BFD求得BF的长,再根据△BEG∽△BFM求得FM的长.
解答 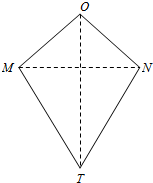 解:(1)猜想:筝形对角线之间的位置关系:垂直.即OT⊥MN.
解:(1)猜想:筝形对角线之间的位置关系:垂直.即OT⊥MN.
证明:连接OT,MN,
在△OMT和△ONT中,
$\left\{\begin{array}{l}{OM=ON}\\{OT=OT}\\{TM=TN}\end{array}\right.$,
∴△OMT≌△ONT(SSS),
∴∠MOT=∠NOT,
∵OM=ON,
∴OT⊥MN(等腰三角形三线合一).
(2)①存在.
由(1)得AC⊥BD,设AC与BD交于点M,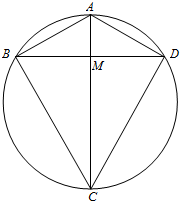
在Rt△AMB中,AB=5,BM=$\frac{1}{2}$BD=4,
∴AM=$\sqrt{A{B}^{2}-B{M}^{2}}$=3,
∵A、B、C、D四点共圆,
∴∠ABC+∠ADC=180°,
又∵△ABC≌△ADC,
∴∠ABC=∠ADC=90°,
∴AC即为所求圆的直径
∵∠BAM=∠BAC,∠ABC=∠AMB=90°,
∴△ABM∽△ACB,
∴$\frac{AB}{AC}$=$\frac{AM}{AB}$,即$\frac{5}{AC}$=$\frac{3}{5}$,
∴AC=$\frac{25}{3}$
∴圆的半径为:$\frac{1}{2}$AC=$\frac{25}{6}$.
②作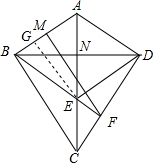 FM⊥AB,作EG⊥AB于G.
FM⊥AB,作EG⊥AB于G.
∵四边形ABED是菱形,
∴AE⊥BD,且BN=$\frac{1}{2}$BD=4,
∴AN=NE=$\sqrt{A{B}^{2}-B{N}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,AE=6.
∴S菱形ABED=$\frac{1}{2}$AE•BD=$\frac{1}{2}$×6×8=24,
又∵S菱形ABED=AB•EG,
∴EG=$\frac{24}{5}$.
∵∠DBF=∠DBF,∠BNE=∠BFD,
∴△BNE∽△BFD,
∴$\frac{BF}{BN}=\frac{BD}{BE}$,即$\frac{BF}{4}=\frac{8}{5}$,
∴BF=$\frac{32}{5}$.
∵GE⊥AB,FM⊥AB,
∴GE∥FM,
∴△BEG∽△BFM,
∴$\frac{FM}{GE}=\frac{BF}{BE}$,即$\frac{FM}{\frac{24}{5}}=\frac{\frac{32}{5}}{5}$,
解得:FM=$\frac{768}{125}$.
点评 本题考查了菱形的判定与性质,以及相似三角形的判定与性质,正确作出辅助线是关键,在初中范围内求线段长的基本方法是解直角三角形和利用三角形相似求解.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
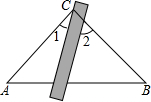 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )| A. | 55° | B. | 45° | C. | 25° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
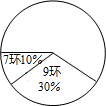 第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:
第17届亚洲运动会于2014年9月19日-10月4日在韩国仁川举行,中国射击队对这次仁川亚运会非常重视,在一次选拔赛中,运动员甲10次射击成绩的统计表和扇形统计图如下:| 命中环数 | 10 | 9 | 8 | 7 |
| 命中次数 | 4 | 3 | 2 | ,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
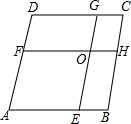 如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )
如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( )| A. | 6.5 | B. | 6 | C. | 5.5 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
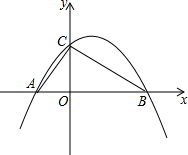 如图,已知抛物线y=ax2+bx+c经过A(-2,0),B(4,0),C(0,3)三点.
如图,已知抛物线y=ax2+bx+c经过A(-2,0),B(4,0),C(0,3)三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com