
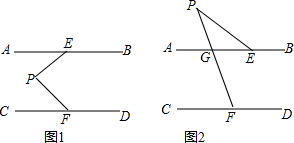
分析 (1)过P点作PG∥AB,根据平行线的性质由PG∥AB得到∠EPG=∠AEP,再根据平行线的性质得PG∥CD,则∠FPG=∠CFP,所以∠AEP+∠CFP=∠EPF;
(2)根据三角形外角的性质得出∠AEP+∠EPF=∠AGP,根据平行线的性质由CD∥AB得到∠APG=∠CFP,所以∠AEP+∠EPF=∠CFP.
解答 (1)证明:过P点作PG∥AB,如图1,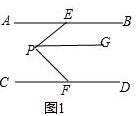
∵PG∥AB,
∴∠EPG=∠AEP,
∵AB∥CD,
∴PG∥CD,
∴∠FPG=∠CFP,
∴∠AEP+∠CFP=∠EPF;
(2)∠AEP+∠EPF=∠CFP,理由如下:
∵∠AEP+∠EPF=∠AGP,
∵CD∥AB,
∴∠APG=∠CFP,
∴∠AEP+∠EPF=∠CFP.
点评 本题考查了平行线的性质:平行于同一条直线的两直线平行;两直线平行,内错角相等.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:填空题
 如图,在平行四边形ABCD中,对角线AC、BD交于O点,AC=6,BD=10,E、F分别是OA、OB的中点.设EF的长为x,则x的取值范围是1<x<4.
如图,在平行四边形ABCD中,对角线AC、BD交于O点,AC=6,BD=10,E、F分别是OA、OB的中点.设EF的长为x,则x的取值范围是1<x<4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
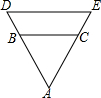 如图,若BC∥DE,$\frac{AB}{AD}$=$\frac{3}{4}$,S△ABC=4,则四边形BCED的面积S四边形DBCE=$\frac{28}{9}$.
如图,若BC∥DE,$\frac{AB}{AD}$=$\frac{3}{4}$,S△ABC=4,则四边形BCED的面积S四边形DBCE=$\frac{28}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
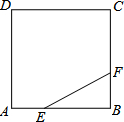 如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线EF向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为( )
如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线EF向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为( )| A. | 12 | B. | 9 | C. | 4$\sqrt{5}$ | D. | 6$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com