
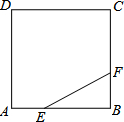
 如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线EF向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为( )
如图,正方形ABCD的边长为3,点E,F分别在边AB、BC上,AE=BF=1,小球P从点E出发沿直线EF向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P所经过的路程长为( )| A. | 12 | B. | 9 | C. | 4$\sqrt{5}$ | D. | 6$\sqrt{5}$ |
分析 根据已知中的点E,F的位置,可知入射角的正切值为$\frac{1}{2}$,通过相似三角形,来确定反射后的点的位置,从而可得反射的次数.再由勾股定理就可以求出小球经过的路径的总长度.
解答 解:根据已知中的点E,F的位置,可知入射角的正切值为$\frac{1}{2}$,第一次碰撞点为F,在反射的过程中,根据入射角等于反射角及平行关系的三角形的相似可得第二次碰撞点为G,在DA上,且DG=$\frac{1}{6}$DA,第三次碰撞点为H,在DC上,且DH=$\frac{1}{3}$DC,第四次碰撞点为M,在CB上,且CM=$\frac{1}{3}$BC,第五次碰撞点为N,在DA上,且AN=$\frac{1}{6}$AD,第六次回到E点,AE=$\frac{1}{3}$AB.
由勾股定理可以得出EF=$\sqrt{5}$,FG=$\frac{3}{2}\sqrt{5}$,GH=$\frac{1}{2}\sqrt{5}$,HM=$\sqrt{5}$,MN=$\frac{3}{2}\sqrt{5}$,NE=$\frac{1}{2}\sqrt{5}$,
故小球经过的路程为:$\sqrt{5}+\frac{3}{2}\sqrt{5}+\frac{1}{2}\sqrt{5}+\sqrt{5}+\frac{3}{2}\sqrt{5}+\frac{1}{2}\sqrt{5}=6\sqrt{5}$,
故选D.
点评 本题主要考查了反射原理与三角形相似知识的运用.通过相似三角形的性质来确定反射后的点的位置,从而可得反射的次数,由勾股定理来确定小球经过的路程,是一道数学物理学科综合试题,难度较大.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
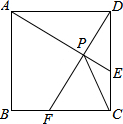 如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动.若AD=2,线段CP的最小值是$\sqrt{5}$-1.
如图,在正方形ABCD中,动点E,F分别从D,C两点同时出发,以相同的速度在边DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动.若AD=2,线段CP的最小值是$\sqrt{5}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
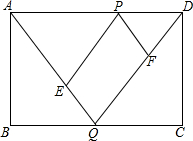 如图,矩形ABCD中,AB=2cm,BC=5cm,两动点P、Q分别同时从顶点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过P作PE∥DQ交AQ于点E,作PF∥AQ交DQ于点F.
如图,矩形ABCD中,AB=2cm,BC=5cm,两动点P、Q分别同时从顶点D、B出发,以1cm/s的速度沿边DA、BC方向向点A、C运动(端点不计),设运动时间为t(s),连接AQ、DQ,过P作PE∥DQ交AQ于点E,作PF∥AQ交DQ于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
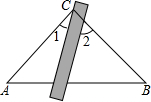 如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )
如图,将三角板与直尺贴在一起,使三角板的直角顶点C(∠ACB=90°)在直尺的一边上.若∠2=55°,则∠1的度数等于( )| A. | 55° | B. | 45° | C. | 25° | D. | 35° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com