
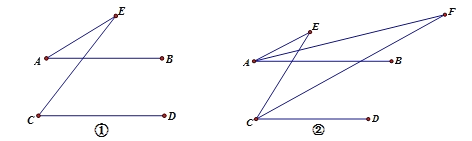
【题目】已知:AF平分∠BAE,CF平分∠DCE.
(1)如图①,已知AB∥CD,求证:∠AEC=∠C-∠A;
(2)如图②,在(1)的条件下,直接写出∠E与∠F的关系.
∠E= (用含有∠F的式子表示)
(3)如图③,BD⊥AB,垂足为B,∠BDC=110°,∠AEC=40°,求∠AFC的度数.
【答案】(1)证明见解析;(2)∠E=2∠F;(3)30°
【解析】
(1)根据平行线的性质推出同位角相等,再根据三角形的外角性质得出结论即可;
(2)根据AF平分∠EAB,CF平分∠ECD,可得∠ECD=2∠FCD,∠EAB=2∠FAM,根据AB∥CD,可得∠FNB=∠FCD,∠EGN=∠ECD,进而证明∠E=2∠F;
(3)如图③,设∠EAM=x°,∠ECD=y°,则可求出∠BMC=140°-x°,由四边形内角和可得∠BMC+∠DCM=160°,从而可得y°-x°=20°;再根据△AEN和△FCN的外角可得∠F+![]() y°=40°+
y°=40°+![]() x°,从而可求出∠F的值.
x°,从而可求出∠F的值.
(1)如图①,

∵AB∥CD,
∴∠EMB=∠ECD,
∵∠AEC+∠EAB=∠EBM,
∴∠AEC+∠EAB=∠ECD,
∴∠AEC=∠C-∠A;
(2)如图②,

(2)∵AF平分∠EAB,CF平分∠ECD,
∴∠ECD=2∠FCD,∠EAB=2∠FAB,
∵AB∥CD,
∴∠FNB=∠FCD,∠EGB=∠ECD,
∵∠FNB是△ANF的外角,
∴∠F=∠FNB-∠FAN=∠FCD-∠FAN
=![]() ∠ECD-
∠ECD-![]() ∠EAB=
∠EAB=![]() ∠EGN-
∠EGN-![]() ∠EAB=
∠EAB=![]() (∠EGN-∠EAB)=
(∠EGN-∠EAB)=![]() ∠E,
∠E,
即∠E=2∠F;
(3)如图③,

设∠EAM=x°,∠ECD=y°,
则∠AME=180°-x°-40°=140°-x°,
即∠BMC=140°-x°,
在四边形BDCM中,∠B=90°,∠BDC=110°,
∴∠BMC+∠DCM=360°-∠B-∠BDC=360°-90°-110°=160°,
∴140°-x°+y°=160°,
∴y°-x°=20°,
∵AF平分∠BAE,CF平分∠DCE,
∴∠EAN=![]() ∠EAM=
∠EAM=![]() x°,∠FCN=
x°,∠FCN=![]() ∠DCM=
∠DCM=![]() y°,
y°,
在△ANE和△FCN中,∠ENF=40°+![]() x°,∠ENF=∠F+
x°,∠ENF=∠F+![]() y°,
y°,
∴∠F+![]() y°=40°+
y°=40°+![]() x°,
x°,
∴∠F=40°+![]() x°-
x°-![]() y°=40°-
y°=40°-![]() (y°-x°)=40°-
(y°-x°)=40°-![]() ×20°=30°.
×20°=30°.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案科目:初中数学 来源: 题型:
【题目】我们自从有了用字母表示数,发现表达有关的数和数量关系更加简洁明了,从而更助于我们发现更多有趣的结论,请你按要求试一试。
(1)用代数式表示:
①a与b的差的平方;②a与b两数平方和与a、b两数积的2倍的差;
(2)当a=3,b=-2时,求第(1)题中①②所列的代数式的值;
(3)由第(2)题的结果,你发现了什么等式?
(4)利用你发现的结论:求20182-4036×2017+20172的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
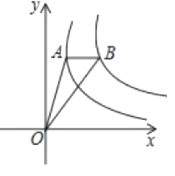
【题目】如图,点A是反比例函数y![]() =
=![]() (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y
(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y![]() =
=![]() (x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为___.
(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字1和-2;乙袋中有三个完全相同的小球,分别标有数字-1、0和2.小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点A的坐标为(x,y).
(1)请用表格或树状图列出点A所有可能的坐标;
(2)求点A在反比例函数y=![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
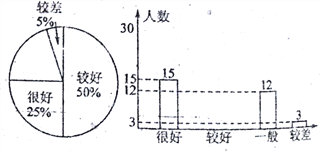
【题目】我国北方又进入了交通事故频发的季节,为此,某校在全校2000名学生中随机抽取一部分人进行“交通安全”知识问卷调查活动,对问卷调查成绩按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了如下扇形统计图和条形统计图.
(1)本次活动共抽取了多少名同学?
(2)补全条形统计图;
(3)根据以上调查结果分析,估计该校2000名学生中,对“交通安全”知识了解一般的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果![]() ,那么
,那么![]() 的值是( )
的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线l1:![]() 分别与x轴、y轴交于点B、C,且与直线l2:
分别与x轴、y轴交于点B、C,且与直线l2:![]() 交于点A.
交于点A.
(1)求出点A的坐标
(2)若D是线段OA上的点,且△COD的面积为12,求直线CD的解析式
(3)在(2)的条件下,设P是射线CD上的点,在平面内是否存在点Q,使以O、C、P、Q为顶点的四边形是菱形?若存在,直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小明父子晨起锻炼身体,两人同时从家出发,小明跑步的速度为每分钟200米,爸爸跑步速度是150米,出发后15分钟后,小明到达广场,立即以一定的速度按原路线返回,3分钟后与爸爸相遇,爸爸与小明仍按小明返回时的速度返回家,下面的图象反应的是父子两人离家的距离与离家时间的关系,观察图回答问题;
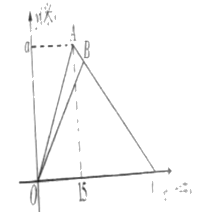
(1)图中a=________________,图中B的坐标为_________________;
(2)求返回时直线AC的解析式:
(3)求运动过程中父子两人何时相距250米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级全体学生在5名教师的带领下去公园秋游,公园的门票为每人30元.现有两种优惠方案,甲方案:带队老师免费,学生按8折收费;乙方案:师生都按7.5折收费.
(1)若有n名学生,用含n的代数式表示两种优惠方案各需多少元?
(2)当n=70时,采用哪种方案更优惠?
(3)当n=100时,采用哪种方案更优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com