
【题目】我们自从有了用字母表示数,发现表达有关的数和数量关系更加简洁明了,从而更助于我们发现更多有趣的结论,请你按要求试一试。
(1)用代数式表示:
①a与b的差的平方;②a与b两数平方和与a、b两数积的2倍的差;
(2)当a=3,b=-2时,求第(1)题中①②所列的代数式的值;
(3)由第(2)题的结果,你发现了什么等式?
(4)利用你发现的结论:求20182-4036×2017+20172的值.
【答案】(1)①(a-b)2;②a2+b2-2ab;(2)当a=3,b=-2时,(a-b)2=![]() 25;(3)(a-b)2=a2+b2-2ab;(4)1.
25;(3)(a-b)2=a2+b2-2ab;(4)1.
【解析】
(1)根据a、b的关系分别列式即可;
(2)把a、b的值代入代数式进行计算即可得解;
(3)根据计算结果相等写出等式;
(4)利用(3)的等式进行计算即可得解.
解:(1)①(a-b)2;②a2+b2-2ab;
(2)当a=3,b=-2时,(a-b)2=![]() 25;
25;
a2+b2-2ab=9+4-2![]() 25;
25;
(3)(a-b)2=a2+b2-2ab;
(4)20182-4036×2017+20172=20182-2×2018×2017+20172=(2018-2017)2=1.


科目:初中数学 来源: 题型:
【题目】某商店准备购进一批电冰箱和空调,每台电冰箱的进价比每台空调的进价多400元,商店用8000元购进电冰箱的数量与用6400元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)已知电冰箱的销售价为每台2100元,空调的销售价为每台1750元.若商店准备购进这两种家电共100台,其中购进电冰箱x台(33≤x≤40),那么该商店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
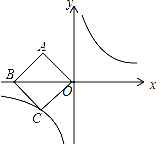
【题目】如图,在平面直角坐标系中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为4![]() ,点B在x负半轴上,反比例函数的图象经过C点.
,点B在x负半轴上,反比例函数的图象经过C点.
(1)求该反比例函数的解析式;
(2)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了弘扬中华传统文化,了解学生整体阅读能力,组织全校的1000名学生进行一次阅读理解大赛.从中抽取部分学生的成绩进行统计分析,根据测试成绩绘制了频数分布表和频数分布直方图:
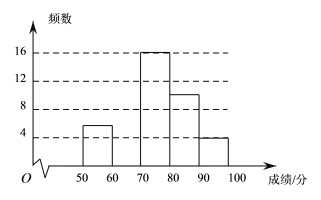
分组/分 | 频数 | 频率 |
50≤x<60 | 6 | 0.12 |
60≤x<70 |
| 0.28 |
70≤x<80 | 16 | 0.32 |
80≤x<90 | 10 | 0.20 |
90≤x≤100 | 4 | 0.08 |
(1)频数分布表中的![]() ;
;
(2)将上面的频数分布直方图补充完整;
(3)如果成绩达到90及90分以上者为优秀,可推荐参加决赛,估计该校进入决赛的学生大约有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]() ,点
,点![]() .
.
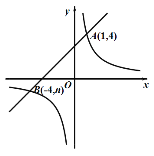
(1)求k和b的值;
(2)连接OA、OB,求![]() 的面积;
的面积;
(3)利用图像,直接写出![]() 时x的取值范围.
时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级数学小组在课外活动中,研究了同一坐标系中两个反比例函数![]() 与
与![]() (
(![]() )在第一象限图像的性质,经历了如下探究过程:
)在第一象限图像的性质,经历了如下探究过程:
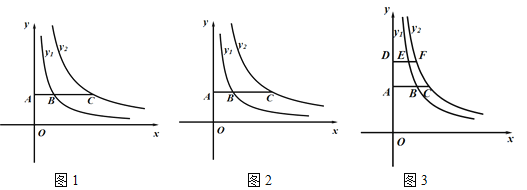
操作猜想:(1)如图1,当![]() ,
,![]() 时,在y轴的正半轴上取一点A作x轴的平行线交
时,在y轴的正半轴上取一点A作x轴的平行线交![]() 于点B,交
于点B,交![]() 于点C.当OA=1时,
于点C.当OA=1时,![]() = ;当OA=3时,
= ;当OA=3时,![]() = ;当OA=a时,猜想
= ;当OA=a时,猜想![]() = .
= .
数学思考:(2)在y轴的正半轴上任意取点A作x轴的平行线,交![]() 于点B、交
于点B、交![]() 于点C,请用含
于点C,请用含![]() 、
、![]() 的式子表示
的式子表示![]() 的值,并利用图2加以证明.
的值,并利用图2加以证明.
推广应用:(3)如图3,若![]() ,
,![]() ,在y轴的正半轴上分别取点A、D(OD>OA)作x轴的平行线,交
,在y轴的正半轴上分别取点A、D(OD>OA)作x轴的平行线,交![]() 于点B、E,交
于点B、E,交![]() 于点C、F,是否存在四边形ADFB是正方形?如果存在,求OA的长和点B的坐标;如果不存在,请说明理由.
于点C、F,是否存在四边形ADFB是正方形?如果存在,求OA的长和点B的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个含有30°角的完全相同的三角板ABC和DEF沿直线l滑动,下列说法错误的是( )
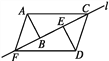
A. 四边形ACDF是平行四边形 B. 当点E为BC中点时,四边形ACDF是矩形
C. 当点B与点E重合时,四边形ACDF是菱形 D. 四边形ACDF不可能是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运输公司承担了某标段的土方运输任务,公司已派出大小两种型号的渣土运输车运输土方,已知2辆大型渣土运输车与3辆小型渣土运输车每次共35吨,3辆大型渣土运输车和2辆小型渣土运输车每次共运40吨.
(1)一辆大型渣土运输车和一辆小型渣土运输车每次各运土方多少吨?
(2)该运输公司决定派出大小两种型号的渣土运输车共20辆参与运输土方,若每次运输土方总量不小于150吨,问该运输公司最多派出几辆小型渣土运输车?
查看答案和解析>>
科目:初中数学 来源: 题型:
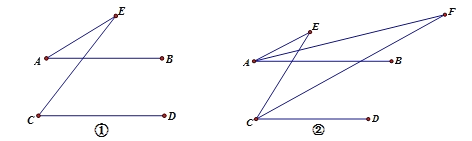
【题目】已知:AF平分∠BAE,CF平分∠DCE.
(1)如图①,已知AB∥CD,求证:∠AEC=∠C-∠A;
(2)如图②,在(1)的条件下,直接写出∠E与∠F的关系.
∠E= (用含有∠F的式子表示)
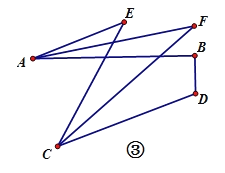
(3)如图③,BD⊥AB,垂足为B,∠BDC=110°,∠AEC=40°,求∠AFC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com