
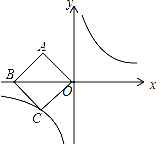
【题目】如图,在平面直角坐标系中,正方形ABCO的对角线BO在x轴上,若正方形ABCO的边长为4![]() ,点B在x负半轴上,反比例函数的图象经过C点.
,点B在x负半轴上,反比例函数的图象经过C点.
(1)求该反比例函数的解析式;
(2)若点P是反比例函数上的一点,且△PBO的面积恰好等于正方形ABCO的面积,求点P的坐标.
【答案】(1)反比例函数解析式为y=![]() ;(2)点P的坐标为(2,8)或(﹣2,﹣8).
;(2)点P的坐标为(2,8)或(﹣2,﹣8).
【解析】试题分析:(1)连接AC,交x轴于点D,由四边形ABCO为正方形,得到对角线互相平分且垂直,四条边相等,根据正方形的边长,利用勾股定理求出CD,OD的长,确定出C坐标,代入反比例解析式求出k的值,即可确定出解析式;
(2)分两种情况考虑:若P1在第一象限的反比例函数图象上,连接P1B,P1O,根据△P1BO的面积恰好等于正方形ABCO的面积,利用三角形面积公式求出P1的纵坐标,代入反比例解析式即可确定出P1的坐标;若P2在第三象限反比例图象上,连接OP2,BP2,同理确定出P2坐标即可.
试题解析:解:(1)连接AC,交x轴于点D.∵四边形ABCO为正方形,∴AD=DC=OD=BD,且AC⊥OB.∵正方形ABCO的边长为4![]() ,∴DC=OD=
,∴DC=OD=![]() =4,∴C(﹣4,﹣4),把C坐标代入反比例函数解析式得:k=16,则反比例函数解析式为y=
=4,∴C(﹣4,﹣4),把C坐标代入反比例函数解析式得:k=16,则反比例函数解析式为y=![]() ;
;
(2)∵正方形ABCO的边长为4![]() ,∴正方形ABCO的面积为32,分两种情况考虑:
,∴正方形ABCO的面积为32,分两种情况考虑:
若P1在第一象限的反比例函数图象上,连接P1B,P1O.∵S△P1BO=![]() BO|yP|=S正方形ABCO=32,而OB=
BO|yP|=S正方形ABCO=32,而OB=![]() CO=8,∴
CO=8,∴![]() ×8×|yP|=32,∴yP1=8,把y=8代入反比例函数解析式得:x=2,此时P1坐标为(2,8);
×8×|yP|=32,∴yP1=8,把y=8代入反比例函数解析式得:x=2,此时P1坐标为(2,8);
若P2在第三象限反比例图象上,连接OP2,BP2,同理得到yP2=﹣8,把y=﹣8代入反比例函数解析式得:x=﹣2,此时P2(﹣2,﹣8).
综上所述:点P的坐标为(2,8)或(﹣2,﹣8).


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
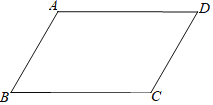
【题目】有下列命题
①一组对边平行,一组对角相等的四边形是平行四边形.
②两组对角分别相等的四边形是平行四边形.
③一组对边相等,一组对角相等的四边形是平行四边形.
④一组对边平行,一条对角线被另一条对角线平分的四边形是平行四边形.
(1)上述四个命题中,是真命题的是 (填写序号);
(2)请选择一个真命题进行证明.(写出已知、求证,并完成证明)
已知: .
求证: .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1).
(1)若多项式的值与字母x的取值无关,求a、b的值.
(2)在(1)的条件下,先化简多项式3(a2﹣ab+b2)﹣(3a2+ab+b2),再求它的值.
(3)在(1)的条件下,求(b+a2)+(2b+![]() a2)+(3b+
a2)+(3b+![]() a2)+…+(9b+
a2)+…+(9b+![]() a2)的值.
a2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
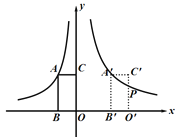
【题目】如图,在平面直角坐标系中,矩形ABOC的两边在坐标轴上,OB=1,点A在函数![]() (x<0)的图像上,将此矩形向右平移3个单位长度到
(x<0)的图像上,将此矩形向右平移3个单位长度到![]() 的位置,此时点
的位置,此时点![]() 在函数
在函数![]() (x>0)的图像上,
(x>0)的图像上,![]() 与此图像交于点P,则点P的坐标是_________.
与此图像交于点P,则点P的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们自从有了用字母表示数,发现表达有关的数和数量关系更加简洁明了,从而更助于我们发现更多有趣的结论,请你按要求试一试。
(1)用代数式表示:
①a与b的差的平方;②a与b两数平方和与a、b两数积的2倍的差;
(2)当a=3,b=-2时,求第(1)题中①②所列的代数式的值;
(3)由第(2)题的结果,你发现了什么等式?
(4)利用你发现的结论:求20182-4036×2017+20172的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
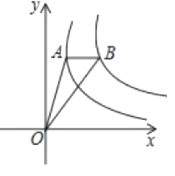
【题目】如图,点A是反比例函数y![]() =
=![]() (x>0)图象上一点,过点A作x轴的平行线,交反比例函数y
(x>0)图象上一点,过点A作x轴的平行线,交反比例函数y![]() =
=![]() (x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为___.
(x>0)的图象于点B,连接OA、OB,若△OAB的面积为2,则k的值为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com