
【题目】某校八年级数学小组在课外活动中,研究了同一坐标系中两个反比例函数![]() 与
与![]() (
(![]() )在第一象限图像的性质,经历了如下探究过程:
)在第一象限图像的性质,经历了如下探究过程:
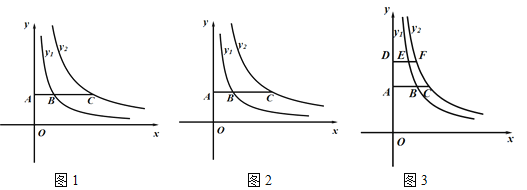
操作猜想:(1)如图1,当![]() ,
,![]() 时,在y轴的正半轴上取一点A作x轴的平行线交
时,在y轴的正半轴上取一点A作x轴的平行线交![]() 于点B,交
于点B,交![]() 于点C.当OA=1时,
于点C.当OA=1时,![]() = ;当OA=3时,
= ;当OA=3时,![]() = ;当OA=a时,猜想
= ;当OA=a时,猜想![]() = .
= .
数学思考:(2)在y轴的正半轴上任意取点A作x轴的平行线,交![]() 于点B、交
于点B、交![]() 于点C,请用含
于点C,请用含![]() 、
、![]() 的式子表示
的式子表示![]() 的值,并利用图2加以证明.
的值,并利用图2加以证明.
推广应用:(3)如图3,若![]() ,
,![]() ,在y轴的正半轴上分别取点A、D(OD>OA)作x轴的平行线,交
,在y轴的正半轴上分别取点A、D(OD>OA)作x轴的平行线,交![]() 于点B、E,交
于点B、E,交![]() 于点C、F,是否存在四边形ADFB是正方形?如果存在,求OA的长和点B的坐标;如果不存在,请说明理由.
于点C、F,是否存在四边形ADFB是正方形?如果存在,求OA的长和点B的坐标;如果不存在,请说明理由.
【答案】(1)2;2;2;(2)![]() ,证明见解析;(3)OA=4,点B的坐标为(2,4).
,证明见解析;(3)OA=4,点B的坐标为(2,4).
【解析】
(1)只需根据ABOA=2及ACOA=6就可解决问题;
(2)由ABOA=k1及ACOA=k2可得BCOA=k2-k1,就可得到![]() ;
;
(3)设点B的坐标为(a,b)(a>0,b>0),则有DF=DA=AB=a,OA=b,从而可得到点F的坐标为(a,a+b).由k2=12及![]() 可求得k1=8.然后根据点B在y=
可求得k1=8.然后根据点B在y=![]() 图象上,点F在y=
图象上,点F在y=![]() 图象上,可得到ab=8,a(a+b)=12,从而求出a、b的值,就可解决问题.
图象上,可得到ab=8,a(a+b)=12,从而求出a、b的值,就可解决问题.
(1)当OA=1时,由ABOA=2得AB=2,由ACOA=6得AC=6,则有BC=AC-AB=4,所以![]() ;
;
当OA=3时,由ABOA=2得AB=![]() ,由ACOA=6得AC=2,则有BC=AC-AB=
,由ACOA=6得AC=2,则有BC=AC-AB=![]() ,所以
,所以![]() ;
;
当OA=a时,猜想:![]() .
.
(2)![]() .
.
证明:∵ABOA=k1,ACOA=k2,
∴ACOA-ABOA=BCOA=k2-k1,
∴![]() .
.
(3)若四边形ADFB是正方形,
设点B的坐标为(a,b)(a>0,b>0),
则有DF=DA=AB=a,OA=b,OD=a+b,
∴点F的坐标为(a,a+b).
∵k2=12,![]() ,
,
∴![]() ,
,
解得:k1=8.
∵点B在y=![]() 图象上,点F在y=
图象上,点F在y=![]() 图象上,
图象上,
∴ab=8,a(a+b)=12,
∴a2=12-8=4/span>,
∴a=2,
∴b=4,
∴OA=4,点B的坐标为(2,4).


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知多项式(2x2+ax﹣y+6)﹣(2bx2﹣3x+5y﹣1).
(1)若多项式的值与字母x的取值无关,求a、b的值.
(2)在(1)的条件下,先化简多项式3(a2﹣ab+b2)﹣(3a2+ab+b2),再求它的值.
(3)在(1)的条件下,求(b+a2)+(2b+![]() a2)+(3b+
a2)+(3b+![]() a2)+…+(9b+
a2)+…+(9b+![]() a2)的值.
a2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们自从有了用字母表示数,发现表达有关的数和数量关系更加简洁明了,从而更助于我们发现更多有趣的结论,请你按要求试一试。
(1)用代数式表示:
①a与b的差的平方;②a与b两数平方和与a、b两数积的2倍的差;
(2)当a=3,b=-2时,求第(1)题中①②所列的代数式的值;
(3)由第(2)题的结果,你发现了什么等式?
(4)利用你发现的结论:求20182-4036×2017+20172的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与探索:将连续的奇数 1,3,5,7…排列成如下的数表,用十字框框出 5 个数(如图)
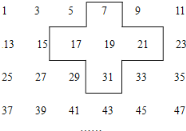
(1)若将十字框上下左右平移,但一定要框住数列中的 5 个数,若设中间的数为 a,用 a 的代数式表示十字框框住的 5 个数字之和;
(2)十字框框住的 5 个数之和能等于 285 吗?若能,分别写出十字框框住的 5 个数;若不能,请说明理由;
(3)十字框框住的 5 个数之和能等于 365 吗?若能,分别写出十字框框住的 5 个数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图的名称;

视图 视图
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果![]() ,那么
,那么![]() 的值是( )
的值是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com