
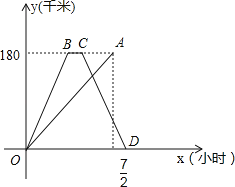
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?
【答案】(1)快车、慢车速度分别为120千米/时,60千米/时;(2)y=﹣120x+420(2≤x≤![]() );(3)两车出发后经过
);(3)两车出发后经过![]() 或
或![]() 或
或![]() 小时相距90千米的路程
小时相距90千米的路程
【解析】试题分析:(1)根据路程与相应的时间,求得慢车的速度,再根据慢车速度是快车速度的一半,求得快车速度;
(2)先求得点C的坐标,再根据点D的坐标,运用待定系数法求得CD的解析式;
(3)分三种情况:在两车相遇之前;在两车相遇之后;在快车返回之后,分别求得时间即可.
试题解析:
(1)快车速度:180×2÷(![]() )=120千米/时,
)=120千米/时,
慢车速度:120÷2=60千米/时;
(2)快车停留的时间:![]() ﹣
﹣![]() ×2=
×2=![]() (小时),
(小时),
![]() +
+![]() =2(小时),即C(2,180),
=2(小时),即C(2,180),
设CD的解析式为:y=kx+b,则
将C(2,180),D(![]() ,0)代入,得
,0)代入,得
 ,
,
解得![]() ,
,
∴快车返回过程中y(千米)与x(小时)的函数关系式为y=﹣120x+420(2≤x≤![]() );
);
(3)相遇之前:120x+60x+90=180,
解得x=![]() ;
;
相遇之后:120x+60x﹣90=180,
解得x=![]() ;
;
快车从甲地到乙地需要180÷120=![]() 小时,
小时,
快车返回之后:60x=90+120(x﹣![]() ﹣
﹣![]() )
)
解得x=![]()
综上所述,两车出发后经过![]() 或
或![]() 或
或![]() 小时相距90千米的路程.
小时相距90千米的路程.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,∠BOC=60°,射线OM平分∠AOC,ON平分∠BOC。
(1)求∠MON的度数;
(2)如果(1)中,∠AOB=α,∠BOC=β(β为锐角),其他条件不变,求∠MON的度数;
(3)从(1)、(2)的结果中,你能得到什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生会为了解本年级600名学生的睡眠情况,将同学们某天的睡眠时长t(小时)分为A,B,C,D,E(A:9≤t≤24;B:8≤t<9;C:7≤t<8;D:6≤t<7;E:0≤t<6)五个选项,进行了一次问卷调查,随机抽取n名同学的调查问卷并进行了整理,绘制成如下条形统计图,根据统计图提供的信息解答下列问题:
(1)求n的值;
(2)根据统计结果,估计该年级600名学生中睡眠时长不足7小时的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=110°,点E是菱形ABCD内一点,连结CE绕点C顺时针旋转110°,得到线段CF,连结BE,DF,若∠E=86°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
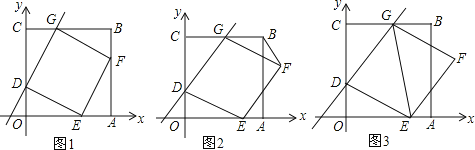
【题目】在平面直角坐标系xOy中,边长为6的正方形OABC的顶点A,C分别在x轴和y轴的正半轴上,直线y=mx+2与OC,BC两边分别相交于点D,G,以DG为边作菱形DEFG,顶点E在OA边上.
(1)如图1,顶点F在边AB上,当CG=OD时,
求m的值;
菱形DEFG是正方形吗?如果是请给予证明.
(2)如图2,连接BF,设CG=a,△FBG的面积为S,求S与a的函数关系式;
(3)如图3,连接GE,当GD平分∠CGE时,请直接写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知2辆A型车和1辆B型车载满货物一次可运货10吨.用1辆A型车和2辆B型车载满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆和B型车b辆,一次运完,且每辆车都满载货物.根据以上信息解答下列问题:
(1)1辆A型车和1辆B型车载满货物一次分别可运货物多少吨?
(2)请帮助物流公司设计租车方案
(3)若A型车每辆车租金每次100元,B型车每辆车租金每次120元.请选出最省钱的租车方案,并求出最少的租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
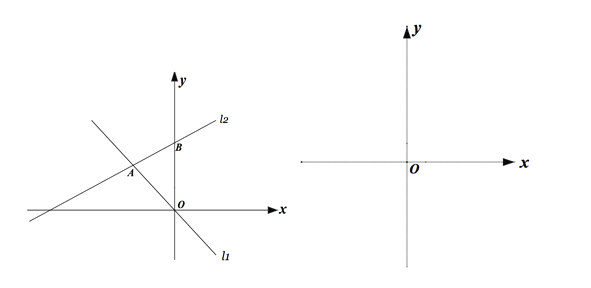
【题目】如图,在平面直角坐标系中,直线l1的解析式为y=-x,直线l2与l1交于A点(a,-a)与,与y轴交于点B(0,b),其中a,b满足(a+2)2+![]() =0 .
=0 .
(1)求直线l2放入解析式;
(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;
(3)已知平行于y轴且位于y轴左侧有一动直线,分别与![]() ,
, ![]() 交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com