
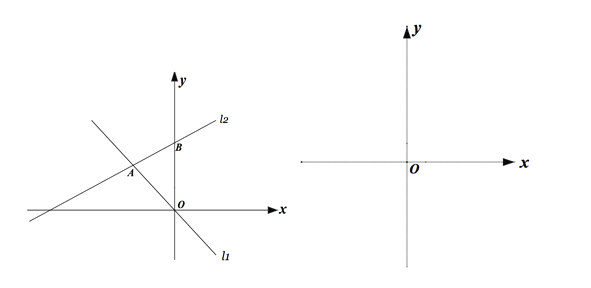
【题目】如图,在平面直角坐标系中,直线l1的解析式为y=-x,直线l2与l1交于A点(a,-a)与,与y轴交于点B(0,b),其中a,b满足(a+2)2+![]() =0 .
=0 .
(1)求直线l2放入解析式;
(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标;
(3)已知平行于y轴且位于y轴左侧有一动直线,分别与![]() ,
, ![]() 交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
交于点M、N,且点M在点N的下方,点Q为y轴上一动点,且△MNQ为等腰直角三角形,请直接写出满足条件的点Q的坐标.
【答案】(1) y=![]() x+3(2)P1(-2,5)P2(-8,5)(3)Q1(0,
x+3(2)P1(-2,5)P2(-8,5)(3)Q1(0, ![]() )Q2(0,
)Q2(0, ![]() )Q3(0,
)Q3(0, ![]() ).
).
【解析】试题分析:(1)根据已知求出A、B两点坐标,然后利用待定系数法即可求出l2的解析式;
(2)由S△BAO=S△PAO,可知点P到AO的距离与点B到AO的距离相等,且点P位于l1两侧,分情况讨论即可得;
(3)设动直线为x=t,由题可得-2<t<0,分三种情况讨论即可得.
试题解析:(1)由题意得:a+2=0,b+3=0,所以a=-2,b=3,
则点A(-2,2),B(0,3),
设l2的解析式为y=kx+3,代入(-2,2),2=-2k+3,解得k=![]() ,
,
∴l2的解析式为:y=![]() x+3;
x+3;
(2)∵S△BAO=S△PAO,则点P到AO的距离与点B到AO的距离相等,且点P位于l1两侧;
当点P在l1的右侧时,设点P为P1,且P1B//l1,
则P1B的解析式为:y=-x+3,
由![]() 得:P1(-2,5),
得:P1(-2,5),
当点P在l1的左侧时,设点P为P2,
设直线y=5与l1,交于点M,则点M(-5,5),且点M为P1P2中点,则P2(-8,5),
综上:P1(-2,5)P2(-8,5);
(3)设动直线为x=t,由题可得-2<t<0,
则M(t,-t),N(t, ![]() t+3)),MN =
t+3)),MN =![]() t+3,
t+3,
当NM⊥NQ且NM=NQ时,Q(0, ![]() t+3)由
t+3)由![]() t+3=-t,解得t=
t+3=-t,解得t=![]() ,此时Q1(0,
,此时Q1(0, ![]() ),
),
当MN⊥MQ且MN=MQ时,Q(0,-t)由![]() t+3=-t,解得t=
t+3=-t,解得t=![]() ,此时Q2(0,
,此时Q2(0, ![]() )
)
当QN⊥QM且QN=QM时,Q(0, ![]() ),由
),由![]() =-2t,解得t=
=-2t,解得t=![]() ,
,
此时Q3(0, ![]() )
)
综上,Q1(0, ![]() ),Q2(0,
),Q2(0, ![]() ),Q3(0,
),Q3(0, ![]() ).
).


科目:初中数学 来源: 题型:
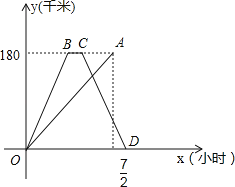
【题目】快、慢两车分别从相距180千米的甲、乙两地同时出发,沿同一路线匀速行驶,相向而行,快车到达乙地停留一段时间后,按原路原速返回甲地.慢车到达甲地比快车到达甲地早![]() 小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
小时,慢车速度是快车速度的一半,快、慢两车到达甲地后停止行驶,两车距各自出发地的路程y(千米)与所用时间x(小时)的函数图象如图所示,请结合图象信息解答下列问题:
(1)请直接写出快、慢两车的速度;
(2)求快车返回过程中y(千米)与x(小时)的函数关系式;
(3)两车出发后经过多长时间相距90千米的路程?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=5,BC=4,以A为圆心,3为半径作圆.试判断:
①点C与⊙A的位置关系;②点B与⊙A的位置关系;③AB中的D点与⊙A的位置关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家窗户上的遮雨罩是一种玻璃钢制品,它的顶部是圆柱侧面的一部分(如图),它的侧面边缘上有两条圆弧(如图3),其中顶部圆弧![]() 的圆心
的圆心![]() 在竖直边缘
在竖直边缘![]() 上,另一条圆弧
上,另一条圆弧![]() 的圆心
的圆心![]() 在水平边缘
在水平边缘![]() 的延长线上,其圆心角为90°,请你根据所标示的尺寸(单位:cm)解决下面的问题(玻璃钢材料的厚度忽略不计,
的延长线上,其圆心角为90°,请你根据所标示的尺寸(单位:cm)解决下面的问题(玻璃钢材料的厚度忽略不计, ![]() 取3.1416).
取3.1416).
(1)计算出弧![]() 所对的圆心角的度数(精确到0.01度)及弧
所对的圆心角的度数(精确到0.01度)及弧![]() 的长度(精确到0.1cm);
的长度(精确到0.1cm);
(2)计算出遮雨罩一个侧面的面积(精确到1cm2);
(3)制做这个遮雨罩大约需要多少平方米的玻璃钢材料(精确到0.1平方米)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一圆形跑道上,甲从A点、乙从B点同时出发,反向而行,8分钟后两人相遇,再过6分钟甲到B点,又过10分钟两人再次相遇.甲环行一周需要的时间是( )

A. 26分钟 B. 28分钟 C. 30分钟 D. 32分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12 cm的正方形ABCD沿其对角线AC剪开,再把ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为32 cm2,则它移动的距离AA′等于( )
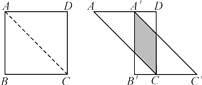
A. 4 cm B. 8 cm C. 6 cm D. 4 cm或8 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句是命题的有( )
①两点之间线段最短;②不平行的两条直线有一个交点;③x 与 y 的和等于 0 吗?④对顶角不相等;⑤互补的两个角不相等;⑥作线段 AB.
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com