
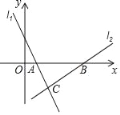
【题目】如图,直线l1的函数表达式为y=﹣2x+2,且与x轴交于点A,直线l2经过点B(5,0)且与l1交于点C,已知点C的横坐标是2.
(1)求点A和点C的坐标;
(2)若在直线l2上存在异于点C的另一点M,使得△ABM与△ABC的面积相等,试求点M的坐标.
(3)在y轴上求点P的坐标,使得PA+PC最小.
【答案】(1)C(2,﹣2);(2)M(8,2);(3)P(0,﹣![]() ).
).
【解析】
(1)利用待定系数法即可解决问题;
(2)利用中点坐标公式计算即可;
(3)作点A关于y轴的对称点A′(-1,0),连接CA′交y轴于P,此时PA+PC的值最小,求出直线CA′的解析式即可解决问题;
解:(1)对于直线y=﹣2x+2,令y=0,得到x=1,
∴A(1,0),
∵点C的横坐标为2,
∴C(2,﹣2);
(2)由题意BC=BM,设M(m,n),
则有![]() =5,
=5, ![]() =0,
=0,
解得m=8,n=2,
∴M(8,2);
(3)作点A关于y轴的对称点A′(﹣1,0),连接CA′交y轴于P,此时PA+PC的值最小,
设最小CA′的解析式为y=kx+b,则有![]()
解得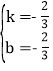
∴直线CA′的解析式为y=﹣![]() x﹣
x﹣![]() ,
,
∴P(0,﹣![]() ).
).


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x与双曲线y=
x与双曲线y= ![]() 相交于A、B两点,BC⊥x轴于点C(﹣4,0).
相交于A、B两点,BC⊥x轴于点C(﹣4,0).
(1)求A、B两点的坐标及双曲线的解析式;
(2)若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴交于点E,且△AOE的面积为10,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上, ![]() =
= ![]() ,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=
,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y= ![]() 的图象过点C,若以CD为边的正方形的面积等于
的图象过点C,若以CD为边的正方形的面积等于 ![]() ,则k的值是.
,则k的值是.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为25和17,则△EDF的面积为( )

A. 4 B. 5 C. 5.5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上有A、B两点,A在B的左侧,已知点B对应的数为2,点A对应的数为a.
(1)若a=﹣3,则线段AB的长为 (直接写出结果);
(2)若点C在线段AB之间,且AC﹣BC=2,求点C表示的数(用含a的式子表示);
(3)在(2)的条件下,点D是数轴上A点左侧一点,当AC=2AD,BD=4BC,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
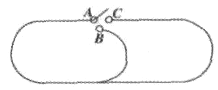
【题目】如图是一个玩具火车轨道,点A有个变轨开关,可以连接点B或点C.小圈轨道的周长是2米,大圈轨道的周长是4米.开始时,点A连接点C,火车从点A出发,按照顺时针方向在轨道上移动,同时变轨开关每隔一分钟变换一次轨道连接.若火车的速度是每分钟10米,则火车第10次回到A点时用了 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24千米,小亮8:00从家出发,骑自行车去姥姥家,妈妈8:30从家出发,乘车沿相同路线去姥姥家.小亮和妈妈的行进路程(千米)与时间(时)的图象如图所示.根据图象得到下列结论,其中错误的是( )
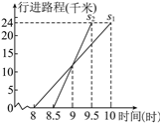
A. 小亮骑自行车的平均速度是12千米/时
B. 妈妈比小亮提前0.5小时到达姥姥家
C. 妈妈在距家12千米处追上小亮
D. 9:30妈妈追上小亮
查看答案和解析>>
科目:初中数学 来源: 题型:
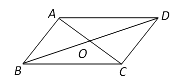
【题目】如图,四边形ABCD中,对角线AC与BD相交于O,在①AB∥CD;②AO=CO;③AD=BC中任意选取两个作为条件,“四边形ABCD是平行四边形”为结论构成命题。
(1)以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例;
(2)写出按题意构成的所有命题中的假命题,并举出反例加以说明.(命题请写成“如果…,那么….”的形式)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com