
【题目】如图,![]() 中,
中,![]() ,
,![]() ,点P从顶点B出发,沿B→C→A以每秒1cm的速度匀速运动到A点,设运动时间为x秒,
,点P从顶点B出发,沿B→C→A以每秒1cm的速度匀速运动到A点,设运动时间为x秒,![]() 长度为y cm.某学习小组对函数y随自变量x的变化而变化的规律进行了探究.下面是他们的探究过程,请补充完整:
长度为y cm.某学习小组对函数y随自变量x的变化而变化的规律进行了探究.下面是他们的探究过程,请补充完整:


(1)通过取点,画图,测量,得到了x(秒)与y(cm)的几组对应值:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
y | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 4.2 | 3.6 | 3.2 | 3.0 | 3.6 | 4.2 | 5.0 |
要求:补全表格中相关数值(保留一位小数);
(2)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当x约为__________时,![]() .
.
【答案】(1) 5.0;3.2,如下表格所示;
(2) 函数图像如下所示:

(3) 2.5秒或8.1秒.
【解析】
(1)在坐标网格中描出表格中的点,找出规律即可得到答案;
(2)描出表格中点后再连线,即可得到函数图像;
(3)分类讨论:当P点在线段BC上时和P点在线段AC上时两种情况,然后再在图像中画出CP的长度随x变化的函数图像,根据两个图像相交即可得到答案.
解:(1)当x=5时,表示P点运动了5秒,路程为5cm,此时BP=5.0cm;
当x=10时,表示P点运动了10秒,路程为10cm,此时CP=10-5=5.0cm,
过B点作BH⊥AC于H点,如下图所示,

由等腰三角形的“三线合一”知:CH=AH=4.0cm.
当P1H=P2H=1cm时,由对称性知道:BP1=BP2
P点位于P1时,所需要的时间为:5+3=8秒
故t=10秒时BP2=BP1=3.2cm.
故表中数据补充如下:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
y | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 4.2 | 3.6 | 3.2 | 3.0 | 3.2 | 3.6 | 4.2 | 5.0 |
故答案为:5.0;3.2.
(2)描点、连线,画出函数图像如下所示:

(3)由题意得:如下图所示:
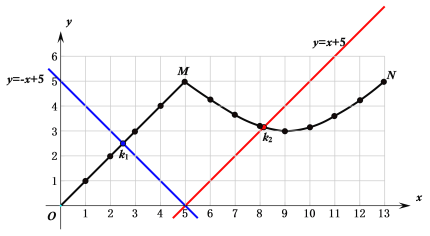
当0≤x≤5时,P点在BC上,此时对应图中的OM段,此时PC=5- x,如图中蓝色线所示,其交点k1即表示BP=CP,此时x =2.5秒;
当5<x≤13时,P点在AC上,此时对应图中的MN段,此时PC= x -5,如图中红色线所示,
其交点k2即表示BP=CP,此时x约为8.1秒.
故答案为:2.5秒或8.1秒.


科目:初中数学 来源: 题型:
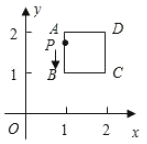
【题目】如图,平面直角坐标系中,在边长为1的正方形![]() 的边上有—动点
的边上有—动点![]() 沿正方形运动一周,
沿正方形运动一周,![]() 则
则![]() 的纵坐标
的纵坐标![]() 与点
与点![]() 走过的路程
走过的路程![]() 之间的函数关系用图象表示大致是( )
之间的函数关系用图象表示大致是( )
A. 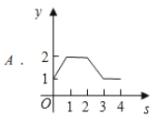 B.
B. 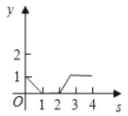 C.
C. 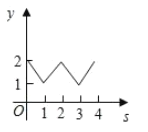 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你知道数学中的整体思想吗?解题中,若把注意力和着眼点放在问题的整体上,多方位思考、联想、探究,进行整体思考、整体加减,能使问题迅速获解.
例题:已知x2+xy=4,xy+y2=-1.求代数式x2-y2的值.
解:将两式相减,得(x2+xy)-(xy+y2)=4-(-1),即x2-y2=5;请用整体思想解答下列问题:
(1)在例题的基础上求(x+y)2的值;
(2)若关于x、y的二元一次方程组![]() 的解也是二元一次方程x+y=6的解,求k的值.
的解也是二元一次方程x+y=6的解,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长江汛期即将来临,为便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),∠BAN=45°.灯A射线自AM顺时针旋转至AN便立即回转,灯B射线自BP顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是3度/秒,灯B转动的速度是1度/秒.假定这一带长江两岸河堤是平行的,即PQ∥MN.如图2,两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作CD⊥AC交PQ于点D,则在转动过程中,求∠BAC与∠BCD的比值,并说明理由.
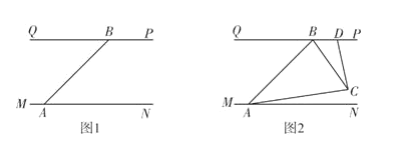
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险. 半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同,问两队的平均速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB∥CD,点P在两平行线之间,点E. F分别在AB、CD上,连接PE,PF.尝试探究并解答:
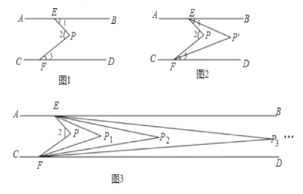
(1)若图1中∠1=36°,∠2=63°,则∠3=___;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2所示,∠1与∠3的平分线交于点P`,若∠2=α,试求∠EP`F的度数(用含α的代数式表示);
(4)如图3所示,在图2的基础上,若∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() ,∠BEP
,∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() …∠BEP
…∠BEP![]() 与∠DFP
与∠DFP![]() 的平分线交于点P
的平分线交于点P![]() ,且∠2=α,直接写出∠EP
,且∠2=α,直接写出∠EP![]() F的度数(用含α的代数式表示).
F的度数(用含α的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织植树活动,按年级将七、八、九年级学生分成三个植树队,七年级植树x棵,八年级种的数比七年级种的数的2倍少26棵,九年级种的树比八年级种的树的一半多42棵.
(1)请用含x的式子表示三个队共种树多少棵.
(2)若这三个队共种树423棵,请你求出这三队各种了多少棵树.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com