
分析 (1)原式变形后,利用同分母分式的加减法则计算即可得到结果;
(2)原式通分并利用同分母分式的加法法则计算即可得到结果;
(3)原式通分并利用同分母分式的减法法则计算即可得到结果;
(4)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果;
(5)原式利用二次根式的乘法法则计算,化简即可得到结果;
(6)原式各项化简后,合并即可得到结果.
解答 解:(1)原式=$\frac{x+3y-x-2y+2x-3y}{(x+y)(x-y)}$=$\frac{2(x-y)}{(x+y)(x-y)}$=$\frac{2}{x+y}$;
(2)原式=$\frac{a-3+6}{(a+3)(a-3)}$=$\frac{a+3}{(a+3)(a-3)}$=$\frac{1}{a-3}$;
(3)原式=$\frac{{x}^{2}-(x+1)(x-1)}{x-1}$=$\frac{1}{x-1}$;
(4)原式=$\frac{3{x}^{2}-6x-{x}^{2}-2x}{(x+2)(x-2)}$•$\frac{(x+2)(x-2)}{2x}$=$\frac{2x(x-4)}{2x}$=x-4;
(5)原式=$\sqrt{\frac{75}{12}}$-2$\sqrt{45}$=$\sqrt{\frac{25}{4}}$-6$\sqrt{5}$=$\frac{5}{2}$-6$\sqrt{5}$;
(6)原式=2$\sqrt{2}$x+2x$\sqrt{2x}$-$\sqrt{2}$x-2$\sqrt{2x}$=$\sqrt{2}$x.
点评 此题考查了分式的混合运算,以及二次根式的混合运算,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
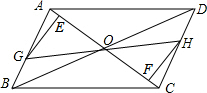 如图,在?ABCD中,点E、F在AC上,且AF=CE,GH过点O分别与AB、CD交于点G、H,试说明:
如图,在?ABCD中,点E、F在AC上,且AF=CE,GH过点O分别与AB、CD交于点G、H,试说明:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
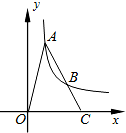 如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6.则k=( )
如图,A、B是双曲线y=$\frac{k}{x}$(k>0)上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6.则k=( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 60 | B. | 80 | C. | 3×220 | D. | 10×220 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com