
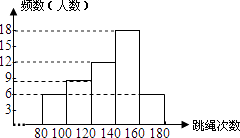
【题目】某校为了了解九年级学生(共450人)的身体素质情况,体育老师对九(1)班的50位学生进行一分钟跳绳次数测试,以测试数据为样本,绘制了如下部分频数分布表和部分频数分布直方图.
组别 | 次数x | 频数(人数) |
A | 80≤x<100 | 6 |
B | 100≤x<120 | 8 |
C | 120≤x<140 | m |
D | 140≤x<160 | 18 |
E | 160≤x<180 | 6 |

请结合图表解答下列问题:
(1)表中的m=;
(2)请把频数分布直方图补完整;
(3)这个样本数据的中位数落在第组;
(4)若九年级学生一分钟跳绳次数(x)合格要求是x≥120,则估计九年级学生中一分钟跳绳成绩不合格的人数.
【答案】
(1)12
(2)
(3)三
(4)
解:∵ ![]() ×100%=72%,
×100%=72%,
∴该班学生测试成绩达标率为72%,
∴九年级学生中一分钟跳绳成绩不合格的人数为:450×(1﹣72%)=126.
【解析】解:(1)6+8+m+18+6=50,
解得m=12;
所以答案是:12;
(2)补全频率分布直方图如下所示: ;
;
(3)∵按照跳绳次数从少到多,第25、26两人都在第三组,
∴中位数落在第三组,
所以答案是:三;
【考点精析】本题主要考查了频数分布直方图和中位数、众数的相关知识点,需要掌握特点:①易于显示各组的频数分布情况;②易于显示各组的频数差别.(注意区分条形统计图与频数分布直方图);中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D在边AB上,连接CD,将△BCD沿CD翻折得到△ECD,使DE∥AC,CE交AB于点F,若∠B=α,则∠ADC的度数是 (用含α的代数式表示).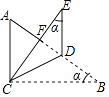
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,tanA= ![]() ,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
,点D是边AC上一点,连接BD,并将△BCD沿BD折叠,使点C恰好落在边AB上的点E处,过点D作DF⊥BD,交AB于点F.
(1)求证:∠ADF=∠EDF;
(2)探究线段AD,AF,AB之间的数量关系,并说明理由;
(3)若EF=1,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,有一Rt△ABC,且A(﹣1,3),B(﹣3,﹣1),C(﹣3,3),已知△A1AC1是由△ABC旋转得到的.
(1)请写出旋转中心的坐标是 , 旋转角是度;
(2)以(1)中的旋转中心为中心,分别画出△A1AC1顺时针旋转90°、180°的三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,∠A=30°,BC=4.若DE是△ABC的中位线,延长DE交∠ACM的平分线于点F,则DF的长为( ) 
A.6
B.7
C.8
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE= ![]() AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
(1)问题发现
①当θ=0°时, ![]() =;
=;
②当θ=180°时, ![]() = .
= .
(2)拓展探究
试判断:当0°≤θ<360°时, ![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
①在旋转过程中,BE的最大值为;
②当△ADE旋转至B、D、E三点共线时,线段CD的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下:
自选项目 | 人数 | 频率 |
立定跳远 | 9 | 0.18 |
三级蛙跳 | 12 | a |
一分钟跳绳 | 8 | 0.16 |
投掷实心球 | b | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
(1)求a,b的值;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中 ![]() 有一名女生的概率.
有一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com