
【题目】某科技开发公司研制出一种新型的产品,每件产品的成本为2400元,销售单价定为3000元,在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获得的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获得的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获得的利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
科目:初中数学 来源: 题型:
【题目】(8分)如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于A(2,3),B(-3,n)两点.
的图象交于A(2,3),B(-3,n)两点.
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,求OP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:32-12=8×1;52-32=8×2;72-52=8×3;…,请用含正整数n的等式表示你所发现的规律:___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
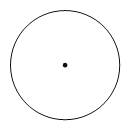
【题目】《九章算术》中记载了这样一道题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代的语言表述为:“如果AB为⊙O的直径,弦CD⊥AB于E,AE=1寸,CD=10寸,那么直径AB的长为多少寸?”请你补全示意图,并求出AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=ax2+bx (a≠0)经过A(3,0)、B(4,4)两点.
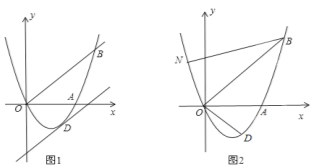
(1)求抛物线的解析式;
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个公共点D,求m的值及点D的坐标;
(3)如图2,若异于点A的点N在抛物线上,且∠NBO=∠ABO,求点N的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若∠α与∠β的两边分别平行,且∠α=(x﹣10)°,∠β=(2x+25)°,则∠α的度数为( )
A. 55° B. 45° C. 45°或55° D. 55°或65°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com