练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，则这两个条件可以是①②（答案不唯一）．（填一组正确的即可）

    分析 由AB=BC得出四边形ABCD是菱形，再由∠ABC=90°，即可得出四边形ABCD是正方形．

    解答 解：这两个条件可以是①②；理由如下：
    ∵四边形ABCD是平行四边形，AB=BC，
    ∴平行四边形ABCD是菱形，
    又∵∠ABC=90°，
    ∴菱形ABCD是正方形；
    故答案为：①②（答案不唯一）．

    点评 此题主要考查了正方形的判定以及矩形、菱形的判定方法，正确掌握正方形的判定方法是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    6．-（2x2y4）3=-8x6y12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．某班有学生50人，某同学根据全班学生的课外活动情况绘制的扇形统计图（如图所示），则参加“其他”活动的人数是10．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．如图所示，点A1、A2、A3在x轴上，且OA1=A1A2=A2A3，分别过点A1、A2、A3作y轴的平行线，与反比例函数y=$\frac{k}{x}$（x＞0）的图象分别交于点B1、B2、B3，分别过点B1、B2、B3作x轴的平行线，分别与y轴交于点C1、C2、C3，连接OB1、OB2、OB3，那么图中阴影部分的面积之和为$\frac{49}{18}$，则k的值为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

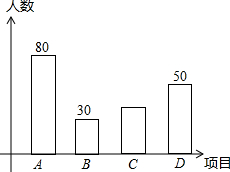    11．某中学开展“阳光体育一小时”活动．根据学校事假情况，决定开设四项运动项目：A：踢毽子；B：篮球；C：跳绳；D：乒乓球．为了解学生最喜欢哪一种运动项目，随机抽取了n名学生进行问卷调查，每位学生在问卷调查时都按要求只选择了其中一种喜欢的运动项目．收回全部问卷后，将收集到的数据整理并绘制成如下的统计图，若参与调查的学生中喜欢A方式的学生的人数占参与调查学生人数的40%．根据统计图提供的信息，解答下列问题：
    （1）求n的值．
    （2）求参与调查的学生中喜欢C的学生的人数．
    （3）根据统计结果，估计该校1800名学生中喜欢C方式的学生比喜欢B方式的学生多的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列命题中，其中正确命题的个数为（　　）个
    ①Rt△ABC中，已知两边长分别为3和4，则第三边为5；
    ②有一个内角等于其他两个内角和的三角形是直角三角形；
    ③三角形的三边分别为a，b，c若a2+c2=b2，则∠C=90°
    ④在△ABC中，∠A：∠B：∠C=1：5：6，则△ABC为直角三角形．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

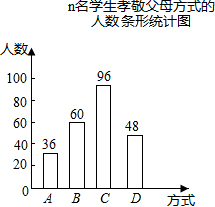    8．某校团委为了了解学生孝敬父母的情况，在全校范围内随机抽取n名学生进行问卷调查．问卷中孝敬父母方式包括：A．为父母洗一次脚；B．帮父母做一次家务；C．给父母买一件礼物；D．其他．每位学生在问卷调查时都按要求只选择了其中一种方式，该校团委收回全部问卷后，将收集到的数据整理并绘制成如下的统计图．
    （1）求n的值．
    （2）四种方式中被选择次数最多的方式为C（用A、B、C、D作答）；选择该种方式的学生人数占被调查的学生人数的百分比为40%．
    （3）根据统计结果，估计该校1600名学生中选择B方式的学生比选择A方式的学生多的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．某市居民生活的用水费用由“城市供水费”与“污水处理费”两部分组成．为了鼓励市民节约用水，其中城市供水费按阶梯式计费：一个月用水10吨以内（包括10吨）的用户，每吨收1.5元；一个月用水超过10吨的用户，10吨水仍按每吨1.5元收费，超过10吨的部分，按每吨a元收费．另外，污水处理费一律按每吨0.65元收取．
    （1）某居民某月用水8吨，应交水费多少元？
    （2）已知小王家某月用水20吨，交用水费用48元．
    ①求a的值；
    ②若某用户某月用水量超过10吨，设用水量为x吨，请你用含x的代数式表示应交的用水费用；
    ③已知某月居民甲比居民乙多用水4吨，两家各自交用水费用后合计为64.2元，求他们这个月分别用水多少吨？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．如图，已知AB∥CD，∠2=140°，则∠1=（　　）
    A．30°B．40°C．45°D．50°

    查看答案和解析>>

    同步练习册答案