
【题目】如图,在Rt△ABC中,∠A=90°,AB=6cm,AC=8cm,以斜边BC上距离B点6cm的点P为中心,把这个三角形按逆时针方向旋转90°至△DEF,则旋转前后两个三角形重叠部分的面积是_______cm2.

【答案】![]()
【解析】
过P作PM⊥AC于M,PN⊥DF于N,由以斜边BC上距离B点6cm的点P为中心,把这个三角形按逆时针方向旋转90°至△DEF,根据旋转的性质得∠KPH=90°,∠KGH=90°,得∠MPN=90°,易证Rt△PCM≌Rt△PFN,得到PM=PN,则四边形PMGN为正方形,Rt△PNK≌Rt△PMH,由PM∥AB,PM:AB=CP:CB,得到PM=![]() ,于是S重叠=S正方形PMGN=(
,于是S重叠=S正方形PMGN=(![]() )2=
)2=![]() .
.
过P作PM⊥AC于M,PN⊥DF于N,如图,

∵以斜边BC上距离B点6cm的点P为中心,把这个三角形按逆时针方向旋转90°至△DEF,
∴∠KPH=90°,∠KGH=90°,
∴∠MPN=90°,
∴∠KPN=∠MPH,
∵PC=PF,∠C=∠F,
∴Rt△PCM≌Rt△PFN,
∴PM=PN,
∴四边形PMGN为正方形,Rt△PNK≌Rt△PMH,
∴S重叠部分=S正方形PMGN,
∵∠A=90°,AB=6,AC=8,
∴BC=10,
而PB=6,则PC=4,
又∵PM∥AB,
∴PM:AB=CP:CB,
∴PM=![]() ,
,
∴S重叠=S正方形PMGN=(![]() )2=
)2=![]() (cm2).
(cm2).
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】边长为a的正方形ABCD中,点E是BD上一点,过点E作EF⊥AE交射线CB于点F,连结CE.
(1)若点F在边BC上(如图);
①求证:CE=EF;
②若BC=2BF,求DE的长.
(2)若点F在CB延长线上,BC=2BF,请直接写出DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省嘉兴市,第20题,8分)如图,一次函数![]() (
(![]() )与反比例函数
)与反比例函数![]() (
(![]() )的图象交于点A(﹣1,2),B(m,﹣1).
)的图象交于点A(﹣1,2),B(m,﹣1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
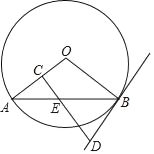
【题目】如图,AB是⊙O的一条弦,E是AB的中点,过点E作EC⊥OA于点C,过点B作⊙O的切线交CE的延长线于点D.
(1)求证:DB=DE;
(2)若AB=12,BD=5,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.
(1)求证:△ABC≌△ADE;
(2)求∠FAE的度数;
(3)求证:CD=2BF+DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学了分式方程的解法,下面是晶晶同学的解题过程:
解方程![]()
解:整理,得:![]() ……………………………………………………第①步
……………………………………………………第①步
去分母,得:![]() ……………………………………………………………第②步
……………………………………………………………第②步
移项,得:![]() …………………………………………………………………第③步
…………………………………………………………………第③步
合并同类项,得![]() ………………………………………………………………第④步
………………………………………………………………第④步
系数化1,得:![]() …………………………………………………………………第⑤步
…………………………………………………………………第⑤步
检验:当![]() 时,
时,![]()
所以原方程的解是![]() ………………………………………………………………第⑥步
………………………………………………………………第⑥步
上述晶晶的解题辻程从第__________步开始出现错误,错误的原因是_________________.请你帮晶晶改正错误,写出完整的解题过程
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济的发展,高铁逐渐成为了主要的交通工具,一般的高铁G字头的高速动车组以D字头的动车组,由大连到北京的G377的平均速度是D31的平均速度的![]() 倍,行驶相同的路程
倍,行驶相同的路程![]() 千米,G377少用
千米,G377少用![]() 个小时。
个小时。
(1)求D31的平均速度。
(2)若以“速度与票价的比值”定义这两种列车的性价比,人们出行都喜欢选择性价比高的方式,现阶段D31票价为![]() 元/张,G377票件为
元/张,G377票件为![]() 元/张,如果你又机会给有关部门提一个合理化建议,使G377得性价比达到D31的性价比,你如何建议,为什么?
元/张,如果你又机会给有关部门提一个合理化建议,使G377得性价比达到D31的性价比,你如何建议,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P(a,b),若点P′的坐标为(a+kb,ka+b)(其中k为常数,且![]() ),则称点P′为点P的“k属派生点”.例如:P(1,4)属派生点为P′(1+2×4,2×1+4),即P′(9,6).
),则称点P′为点P的“k属派生点”.例如:P(1,4)属派生点为P′(1+2×4,2×1+4),即P′(9,6).
(1)点P(-2,3)的“2属派生点”P′的坐标为__________.
(2) 若点P的“3属派生点”P′的坐标为(6,2),求点P的坐标;
(3) 若点P在x轴的正半轴上,点P的“k属派生点”为P′点,且线段PP′的长度为线段OP长度的2倍,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:

如图①,在△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使DE=AD,再连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD),把AB,AC,2AD集中在△ABE中,利用三角形三边的关系即可判断.中线AD的取值范围是___________;
(2)问题解决: 如图②,在△ABC中,D是BC边上的中点,DE⊥DF于点D,DE交AB于点E,DF交AC于点F,连接EF,求证:BE+CF>EF;
(3)问题拓展:如图③,在四边形ABCD中,∠B+∠D=180°,CB=CD,以C为顶点作∠ECF,使得角的两边分别交AB,AD于E、F两点,连接EF,且EF=BE+DF,试探索∠ECF与∠A之间的数量关系,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com