
【题目】某玩具厂要生产500个芭比娃娃,此生产任务由甲、乙、丙三台机器承担,甲机器每小时生产12个,乙、丙两台机器的每小时生产个数之比为4:5.若甲、乙、丙三台机器同时生产,刚好在10小时25分钟完成任务.
(1)求乙、丙两台机器每小时各生产多少个?
(2)由于某种原因,三台机器只能按一定次序循环交替生产,且每台机器在每个循环中只能生产1小时,即每个循环需要3小时.
①若生产次序为甲、乙、丙,则最后一个芭比娃娃由 机器生产完成,整个生产过程共需 小时;
②若想使完成生产任务的时间最少,直接写出三台机器的生产次序及完成生产任务的最少时间.
【答案】(1)乙机器每小时生产16个,丙机器每小时生产20个;(2)乙;31.5(3)使完成生产任务的时间最少,按丙、乙、甲次序交替生产循环共需31小时.
【解析】
(1)设乙机器每小时生产4x个,则丙机器每小时生产5x个,依据甲、乙、丙三台机器同时生产,刚好在10小时25分钟完成任务.列一元一次方程即可解答;
(2)每次循环交替生产48个零件,那么最后一次循环是500除以48的余数,然后按顺序计算即可;
(3)速度快的先做即可.
(1)设乙机器每小时生产4x个,则丙机器每小时生产5x个,10小时25分钟=![]() 小时.依题意得:
小时.依题意得:
![]() (12+4x+5x)=500
(12+4x+5x)=500
解得:x=4,
乙机器每小时生产4x=16个,
丙机器每小时生产5x=20个,
答:乙机器每小时生产16个,丙机器每小时生产20个,
(2)500÷(12+16+20)=10……20,
按甲、乙、丙次序交替生产循环10次,共10×3=30小时,最后20个先由甲生产1小时12个,余下8个由乙生产8÷16=0.5小时,
∴整个生产过程共需30+1+0.5=31.5小时,
故答案为:乙;31.5
(3)使完成生产任务的时间最少,按丙、乙、甲次序交替生产循环,生产循环10次,共10×3=30小时,最后20个由丙生产1小时即可,共需30+1=31小时.
答:使完成生产任务的时间最少,按丙、乙、甲次序交替生产循环共需31小时.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000037毫克可用科学记数法表示为
A. 3.7×10﹣5克 B. 3.7×10﹣6克 C. 37×10﹣7克 D. 3.7×10﹣8克
查看答案和解析>>
科目:初中数学 来源: 题型:
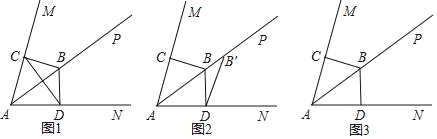
【题目】如图1,已知射线AP是∠MAN的角平分线,点B为射线AP上的一点且AB=10,过点B分别作BC⊥AM于点C,作BD⊥AN于点D,BC=6.
(1)在图1中连接CD交AB于点O.求证:AB垂直平分CD;
(2)从A,B两题中任选一题作答,我选择 题
A.将图1中的△ABC沿射线AP的方向平移得到△ABC,点A、B、C的对应点分别为A′、B′、C′.若平移后点B的对应点B′的位置如图2,连接DB′.
①请在图2中画出此时的△A′B′C′,并在图中标注相应的字母;
②若图2中的DB′∥A′C′,写出平移的距离.
B.将图1中的△ABC沿射线AP的方向平移得到△A′B′C′,点A、B、C的对应点分别为A′、B′、C′.
①在△A′B′C′平移的过程中,若点C′与点D的连线恰好经过点B,请在图3中画出此时的△A′B′C′,并在图中标注相应的字母;
②如图3,点C′与点D的连线恰好经过点B,写出此时平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生体育运动,某市第十七届中小学生田径运动会在市体育场举行,体育场主席台侧面如图所示,若顶棚顶端D与看台底端A的连线和地面垂直,测得顶棚CD的长为12米,∠BAC=30°,∠ACD=45°,求看台AC的长.(结果保留一位小数,参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73)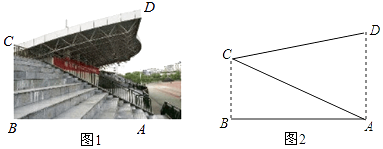
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③180°﹣α﹣β,④360°﹣α﹣β,∠AEC的度数可能是( )
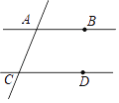
A. ①②③ B. ①②④C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如下图,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34mg/L时,井下3km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井.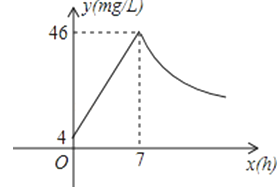
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com