
【题目】如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③180°﹣α﹣β,④360°﹣α﹣β,∠AEC的度数可能是( )
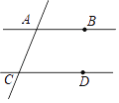
A. ①②③ B. ①②④C. ①③④ D. ①②③④
【答案】B
【解析】
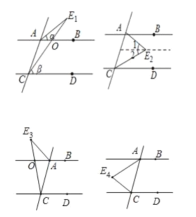
根据E点有4中情况,分四种情况讨论分别画出图形,根据平行线的性质与三角形外角定理求解.
E点有4中情况,分四种情况讨论如下:
由AB∥CD,可得∠AOC=∠DCE1=β
∵∠AE1C=∠BAE1+∠AE1C,
∴∠AE1C=β-α
过点E2作AB的平行线,由AB∥CD,
可得∠1=∠BAE2=α,∠2=∠DCE2=β
∴∠AE2C=α+β
由AB∥CD,可得∠BOE3=∠DCE3=β
∵∠BAE3=∠BOE3+∠AE3C,
∴∠AE3C=α-β
由AB∥CD,可得
∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°-α-β
∴∠AEC的度数可能是①α+β,②α﹣β,④360°﹣α﹣β,故选B.


科目:初中数学 来源: 题型:
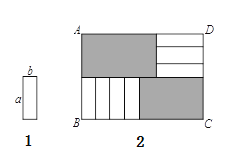
【题目】7张如图的长为![]() ,宽为
,宽为![]() 的小长方形纸片,按如图的方式不重叠地放在矩形
的小长方形纸片,按如图的方式不重叠地放在矩形![]() 内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为
内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为![]() ,当
,当![]() 的长度变化时,则
的长度变化时,则![]() ,
,![]() 满足( )
满足( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A顺时针旋转60°得到△ADE,点C的对应点E恰好落在BA的延长线上,DE与BC交于点F,连接BD.下列结论不一定正确的是( )
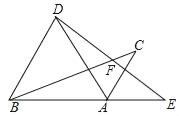
A. AD=BD B. AC∥BD C. DF=EF D. ∠CBD=∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂要生产500个芭比娃娃,此生产任务由甲、乙、丙三台机器承担,甲机器每小时生产12个,乙、丙两台机器的每小时生产个数之比为4:5.若甲、乙、丙三台机器同时生产,刚好在10小时25分钟完成任务.
(1)求乙、丙两台机器每小时各生产多少个?
(2)由于某种原因,三台机器只能按一定次序循环交替生产,且每台机器在每个循环中只能生产1小时,即每个循环需要3小时.
①若生产次序为甲、乙、丙,则最后一个芭比娃娃由 机器生产完成,整个生产过程共需 小时;
②若想使完成生产任务的时间最少,直接写出三台机器的生产次序及完成生产任务的最少时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保”已经成为一种生活理念,同时也带来无限商机.某高科技发展公司投资2000万元成功研制出一种市场需求量较大的低碳高科技产品.已知生产每件产品的成本是40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利为z(万元).(年获利=年销售额﹣生产成本﹣投资)
(1)试写出z与x之间的函数关系式;
(2)请通过计算说明,到第一年年底,当z取最大值时,销售单价x定为多少?此时公司是盈利了还是亏损了?
(3)若该公司计划到第二年年底获利不低于1130万元,请借助函数的大致图象说明,第二年的销售单价x(元)应确定在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年3月30日是全国中小学生安全教育日,某学校为加强学生的安全意识,组织了全校1500名学生参加安全知识竞赛,从中抽取了部分学生成绩(得分取正整数,满分为100分)进行统计.请根据尚未完成的频率分布表和频数分布直方图,解答下列问题:
频率分布表
分数段 | 频数 | 频率 |
50.5~60.5 | 16 | 0.08 |
60.5~70.5 | 40 | 0.2 |
70.5~80.5 | 50 | 0.25 |
80.5~90.5 | m | 0.35 |
90.5~100.5 | 24 | n |
(1)这次抽取了 名学生的竞赛成绩进行统计,其中:m= ,n= ;
(2)补全频数分布直方图;
(3)若成绩在70分以下(含70分)的学生为安全意识不强,有待进一步加强安全教育,则该校安全意识不强的学生约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°
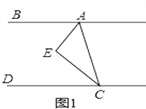
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,在(1)的结论下,当∠E=90°保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?

(3)如图3,在(1)的结论下,P为线段AC上一定点,点Q为直线CD上一动点,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系? (2、3小题只需选一题说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y= ![]() 上,点B在双曲线y=
上,点B在双曲线y= ![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( ) 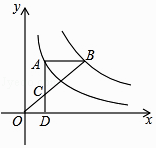
A.6
B.9
C.10
D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com