
【题目】如图,点A在双曲线y= ![]() 上,点B在双曲线y=
上,点B在双曲线y= ![]() (k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( ) 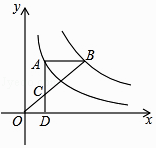
A.6
B.9
C.10
D.12
【答案】D
【解析】解:过点B作BE⊥x轴于E,延长线段BA,交y轴于F, 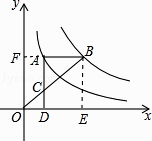
∵AB∥x轴,
∴AF⊥y轴,
∴四边形AFOD是矩形,四边形OEBF是矩形,
∴AF=OD,BF=OE,
∴AB=DE,
∵点A在双曲线y= ![]() 上,
上,
∴S矩形AFOD=4,
同理S矩形OEBF=k,
∵AB∥OD,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AB=2OD,
∴DE=2OD,
∴S矩形OEBF=3S矩形AFOD=12,
∴k=12.
故选D.
过点B作BE⊥x轴于E,延长线段BA,交y轴于F,得出四边形AFOD是矩形,四边形OEBF是矩形,得出S矩形AFOD=4,S矩形OEBF=k,根据平行线分线段成比例定理证得AB=2OD,即OE=3OD,即可求得矩形OEBF的面积,根据反比例函数系数k的几何意义即可求得k的值.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
【题目】花粉的质量很小,一粒某种植物花粉的质量约为0.000037毫克,已知1克=1000毫克,那么0.000037毫克可用科学记数法表示为
A. 3.7×10﹣5克 B. 3.7×10﹣6克 C. 37×10﹣7克 D. 3.7×10﹣8克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③180°﹣α﹣β,④360°﹣α﹣β,∠AEC的度数可能是( )
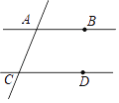
A. ①②③ B. ①②④C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO.在一次矿难事件的调查中现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降.如下图,根据题中相关信息回答下列问题:
(1)求爆炸前后空气中CO浓度y与时间x的函数关系式,并写出相应的自变量取值范围;
(2)当空气中的CO浓度达到34mg/L时,井下3km的矿工接到自动报警信号,这时他们至少要以多少km/h的速度撤离才能在爆炸前逃生?
(3)矿工只有在空气中的CO浓度降到4mg/L及以下时,才能回到矿井开展生产自救,求矿工至少在爆炸后多少小时才能下井.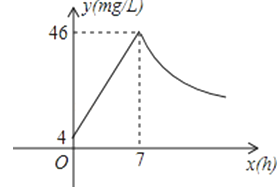
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
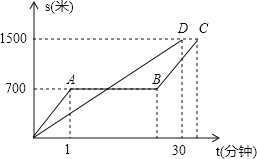
(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中 的路程与时间的关系.赛跑的全程是 米.
(2)兔子在起初每分钟跑 米,乌龟每分钟爬 米.
(3)乌龟用了 分钟追上了正在睡觉的兔子.
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知AD,AE分别是△ADC和△ABC的高和中线,AB=6cm,AC=8cm,BC=10cm,∠CAB=90°.试求:
(1)AD的长;
(2)△ABE的面积;
(3)△ACE和△ABE的周长的差.

查看答案和解析>>
科目:初中数学 来源: 题型:
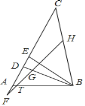
【题目】如图,在△ABC中,BD、BE分别是△ABC的高线和角平分线,点F在CA的延长线上,FH⊥BE交BD于点G,交BC于点H.下列结论:①∠DBE=∠F;②∠BEF=![]() (∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F=
(∠BAF+∠C); ③∠FGD=∠ABE+∠C;④∠F=![]() (∠BAC﹣∠C);其中正确的是_____.
(∠BAC﹣∠C);其中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.

(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A1C1的关系是:______;
(3)画出△ABC中AB边上的中线CE;
(4)平移过程中,线段AC扫过的面积是_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com