
【题目】“低碳环保”已经成为一种生活理念,同时也带来无限商机.某高科技发展公司投资2000万元成功研制出一种市场需求量较大的低碳高科技产品.已知生产每件产品的成本是40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利为z(万元).(年获利=年销售额﹣生产成本﹣投资)
(1)试写出z与x之间的函数关系式;
(2)请通过计算说明,到第一年年底,当z取最大值时,销售单价x定为多少?此时公司是盈利了还是亏损了?
(3)若该公司计划到第二年年底获利不低于1130万元,请借助函数的大致图象说明,第二年的销售单价x(元)应确定在什么范围内?
【答案】
(1)解:依题意知,当销售单价定为x元时,年销售量减少 ![]() (x﹣100)万件,
(x﹣100)万件,
∴y=20﹣ ![]() (x﹣100)=﹣
(x﹣100)=﹣ ![]() x+30,
x+30,
即y与x之间的函数关系式是y=﹣ ![]() x+30.
x+30.
由题意得:
z=y(x﹣40)﹣2000
=(30﹣ ![]() x)(x﹣40)﹣2000
x)(x﹣40)﹣2000
=﹣ ![]() x2+34x﹣3200,
x2+34x﹣3200,
即z与x之间的函数关系是z=﹣ ![]() x2+34x﹣3200
x2+34x﹣3200
(2)解:∵z=﹣ ![]() x2+34x﹣3200,
x2+34x﹣3200,
=﹣ ![]() (x﹣170)2﹣310.
(x﹣170)2﹣310.
∴当x=170时,z取最大值,为﹣310,
即当销售单价为170元,年获利最大,并且第一年年底公司还差310万元就可收回全部投资.
(3)解:第二年的销售单价定为x元时,年获利为:
z=(30﹣ ![]() x)(x﹣40)﹣310=﹣
x)(x﹣40)﹣310=﹣ ![]() x2+34x﹣1510.
x2+34x﹣1510.
当z=1130时,即1130=﹣ ![]() x2+34x﹣1510,
x2+34x﹣1510,
整理得x2﹣340x+26400=0,
解得:x1=120,x2=220.
函数z=﹣ ![]() x2+34x﹣1510的图象大致如图所示,
x2+34x﹣1510的图象大致如图所示,
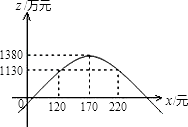
由图象可以看出:当120≤x≤220时,z≥1130.
故第二年的销售单价应确定在不低于120元且不高于220元的范围内.
【解析】(1)当销售单价定为x元时,依据题意可知年销售量减少![]() (x-100),从而可得到y与x之间的函数关系式,进而由题意易得z与x之间的函数关系;
(x-100),从而可得到y与x之间的函数关系式,进而由题意易得z与x之间的函数关系;
(2)利用配方法对z与x的函数关系进行变形,从而可得出当x=170时,z取最大值;即可得出公司是盈利了还是亏损;
(3)首先令获得的利润为1130万元列出方程,然后从而可求得此时x的值,然后依据函数的图形可确定出利润不低于1130万元时,自变量x的取值范围.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
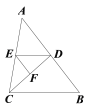
【题目】如图,在△ABC中,已知∠BDC=∠EFD,∠AED=∠ACB.
(1)试判断∠DEF与∠B的大小关系,并说明理由;
(2)若D、E、F分别是AB、AC、CD边上的中点,S△DEF=4,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形AOCB的边长为4,反比例函数的图象过点E(3,4).

(1)求反比例函数的解析式;
(2)反比例函数的图象与线段BC交于点D,直线![]() 过点D,与线段AB相交于点F,求点F的坐标;
过点D,与线段AB相交于点F,求点F的坐标;
(3)连接OF,OE,探究∠AOF与∠EOC的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③180°﹣α﹣β,④360°﹣α﹣β,∠AEC的度数可能是( )
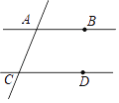
A. ①②③ B. ①②④C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系xOy中,函数y=![]() (x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(x>0)的图象与一次函数y=kx﹣k的图象的交点为A(m,2).
(1)求一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,若P是x轴上一点,且满足△PAB的面积是6,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
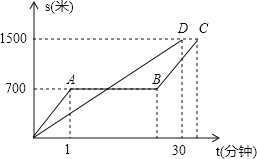
(1)填空:折线OABC表示赛跑过程中 的路程与时间的关系,线段OD表示赛跑过程中 的路程与时间的关系.赛跑的全程是 米.
(2)兔子在起初每分钟跑 米,乌龟每分钟爬 米.
(3)乌龟用了 分钟追上了正在睡觉的兔子.
(4)兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com