
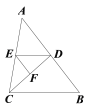
【题目】如图,在△ABC中,已知∠BDC=∠EFD,∠AED=∠ACB.
(1)试判断∠DEF与∠B的大小关系,并说明理由;
(2)若D、E、F分别是AB、AC、CD边上的中点,S△DEF=4,求S△ABC.
【答案】(1)∠DEF=∠B; (2)S△ABC=32.
【解析】
(1)由∠BDC=∠DFE,根据平行线的判定得AB∥EF,则∠ADE=∠DEF,而∠DEF=∠B,所以∠ADE=∠B,由∠AED=∠ACB可判断DE∥BC,然后根据平行线的性质得到∠ADE=∠B;故∠DEF=∠B
(2)D、E、F分别是AB、AC、CD边上的中点,根据三角形面积公式得到S△EDC =2S△DEF,S△ADC =2S△DEC,S△ABC =2S△ADC,可得S△ABC=8S△DEF进行计算即可.
(1)结论:∠DEF=∠B
证明:∵∠BDC=∠DFE,
∴AB∥EF,
∴∠ADE=∠DEF,
∵∠DEF=∠B,
∴∠AED=∠C,
∴DE∥BC,
∴∠ADE=∠B,
∴∠DEF=∠B;
(2)解:∵F为CD的中点,
∴S△DEC =2S△DEF,
同理可得:S△ADC =2S△DEC,S△ABC =2S△ADC,
∵S△DEF=4
∴S△ABC=8S△DEF=8×4=32,


科目:初中数学 来源: 题型:
【题目】某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( )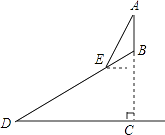
A.50米
B.100米
C.125米
D.150米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(x>0)交于A(2,4),B(a,1),与x轴,y轴分别交于点C,D.
(1)直接写出一次函数y=kx+b的表达式和反比例函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)求证:AD=BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将长为1,宽为![]() 的长方形纸片
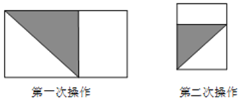
的长方形纸片![]() 如图那样折一下,剪下一个边长等于长方形的宽度的正方形
如图那样折一下,剪下一个边长等于长方形的宽度的正方形![]() 称为第一次操作
称为第一次操作![]() ;再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形
;再把剩下的长方形如图那样折一下,剪下一个边长等于此时长方形宽度的正方形![]() 称为第二次操作
称为第二次操作![]() ;如些反复操作下去,若在第
;如些反复操作下去,若在第![]() 次操作后剩下的长方形为正方形,则操作终止.
次操作后剩下的长方形为正方形,则操作终止.
![]() 第一次操作后,剩下的长方形两边长分别为______和 ;
第一次操作后,剩下的长方形两边长分别为______和 ;![]() 用含
用含![]() 的代数式表示
的代数式表示![]()
![]() 若第二次操作后,剩下的长方形恰好是正方形,则求
若第二次操作后,剩下的长方形恰好是正方形,则求![]() 的值,写出解答过程;
的值,写出解答过程;
![]() 若第三次操作后,剩下的长方形恰好是正方形,画出图形,试求
若第三次操作后,剩下的长方形恰好是正方形,画出图形,试求![]() 的值。
的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
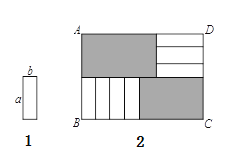
【题目】7张如图的长为![]() ,宽为
,宽为![]() 的小长方形纸片,按如图的方式不重叠地放在矩形
的小长方形纸片,按如图的方式不重叠地放在矩形![]() 内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为
内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为![]() ,当
,当![]() 的长度变化时,则
的长度变化时,则![]() ,
,![]() 满足( )
满足( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
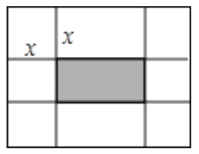
【题目】在槐荫区初中数学文化年的开幕式上,同学们为我们展示了研究性学习“怎样制作一个尽可能大的无盖长方体盒子”.现在有一个长是60cm,宽为40cm的长方形硬纸片做成一个无盖的长方体盒子,于是在长方形的四个角各剪去一个相同的小正方形(如图).
(1)若设这些小正方形的边长为x cm,求图中阴影部分的面积.
(2)当x-5时,求这个盒子的体积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳环保”已经成为一种生活理念,同时也带来无限商机.某高科技发展公司投资2000万元成功研制出一种市场需求量较大的低碳高科技产品.已知生产每件产品的成本是40元,在销售过程中发现:当销售单价定为100元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为x(元),年销售量为y(万件),年获利为z(万元).(年获利=年销售额﹣生产成本﹣投资)
(1)试写出z与x之间的函数关系式;
(2)请通过计算说明,到第一年年底,当z取最大值时,销售单价x定为多少?此时公司是盈利了还是亏损了?
(3)若该公司计划到第二年年底获利不低于1130万元,请借助函数的大致图象说明,第二年的销售单价x(元)应确定在什么范围内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com