解:(1)∵关于x的一元二次方程x
2+2ax+b
2=0有实数根,
∴△=(2a)
2-4b
2≥0,
有a
2-b
2≥0,
(a+b)(a-b)≥0.
∵a>0,b>0,
∴a+b>0,a-b≥0.
∴a≥b.
(2)∵a:b=2:

,
∴设
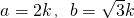
.
解关于x的一元二次方程x
2+4kx+3k
2=0,得x=-k或-3k.
当x
1=-k,x
2=-3k时,由2x
1-x
2=2得k=2.
当x
1=-3k,x
2=-k时,由2x
1-x
2=2得
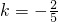
(不合题意,舍去).
∴
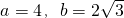
.
(3)当
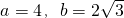
时,
二次函数y=x
2+8x+12与x轴的交点坐标分别为A(-6,0)、C(-2,0),
与y轴交点坐标为B(0,12),顶点坐标D为(-4,-4).
设z=3x-y,则y=3x-z.
画出函数y=x
2+8x+12和y=3x的图象,若直线y=3x平行移动时,如图
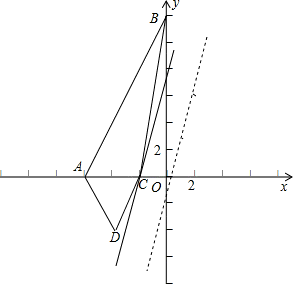
可以发现当直线经过点C时符合题意,此时最大z的值等于-6
分析:(1)根据方程有实数根可以得到其根的判别式为非负数,然后再根据a>0,b>0作出判断即可;
(2)利用a与b的比值分别设出a和b,利用根与系数的关系用设出的未知数表示出方程的两个解,代入的2x
1-x
2=2中求得a与b的值即可;
(3)将上题中求得的a与b的值代入到函数中确定函数的解析式,然后求得与x轴的交点坐标,与y轴的交点坐标和顶点坐标,据此可以求出3x-y的最大值.
点评:本题考查了函数综合知识,函数综合题是初中数学中覆盖面最广、综合性最强的题型.近几年的中考压轴题多以函数综合题的形式出现.解决函数综合题的过程就是转化思想、数形结合思想、分类讨论思想、方程思想的应用过程.

 ,且2x1-x2=2,求a,b的值;
,且2x1-x2=2,求a,b的值; ,
,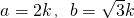 .
.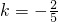 (不合题意,舍去).
(不合题意,舍去).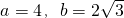 .
.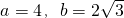 时,
时,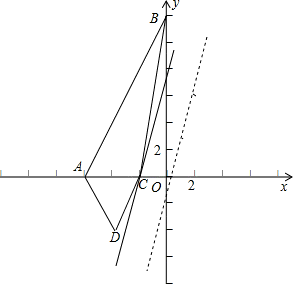


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案 .
. .
.