
分析 题中只告诉两种金笔的总数,并未告诉每种金笔的具体数量,显然不能直接计算;“应付款的总数与永生金笔的总数无关”,购买永生金笔就是有一个固定的比率,即不论有多少支永生金笔,都买这个比率;设学校付的钱数是M,买了英雄金笔x支,则买永生金笔为(143-x)支,还设学校所买的英雄金笔的支数是永生金笔的比率为N,得出M的代数式,然后化简,根据M是固定值,求出N的值,可得M=143×3.78计算即可求解.
解答 解:学校付的钱数是一个固定值,设它为M元,设买英雄金笔x支,则买永生金笔为(143-x)支,还设学校所买的永生金笔的支数是永生金笔的比率为N,则可得方程
(143-x)×3.78+6x×N=M,
化简得:143×3.78+(6N-3.78)×x=M,
其中M为固定值,
由此可知(6N-3.78)×x=0,
所以6N-3.78=0,
解得N=63%,
M=143×3.78=540.54.
答:购买的永生金笔是该商店永生金笔总数的63%,应付款的总数是540.54元.
点评 此题考查了一元一次方程的应用,本题关键是对“应付款的总数与永生金笔的总数无关”这句话的理解,从中得出购买永生金笔就是有一个固定的比率,进而求解.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,P为正方形ABCD的AD边上一点,PE⊥AD交BD于点E点,将△PCD绕C点逆时针方向旋转90°到△FCB的位置,连接PF交BD于Q点.
如图,P为正方形ABCD的AD边上一点,PE⊥AD交BD于点E点,将△PCD绕C点逆时针方向旋转90°到△FCB的位置,连接PF交BD于Q点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
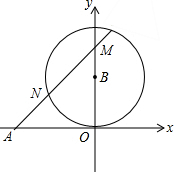 如图,已知A(-2,0),以B(0,1)为圆心,OB长为半径作⊙B,N是⊙B上一个动点,直线AN交y轴于M点,则△AOM面积的最大值是( )
如图,已知A(-2,0),以B(0,1)为圆心,OB长为半径作⊙B,N是⊙B上一个动点,直线AN交y轴于M点,则△AOM面积的最大值是( )| A. | 2 | B. | $\frac{8}{3}$ | C. | 4 | D. | $\frac{16}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com