
ЁОЬтФПЁПЃЈ10ЗжЃЉЃЈ1ЃЉЁОЮЪЬтЗЂЯжЁПаЁУїгіЕНетбљвЛИіЮЪЬтЃК
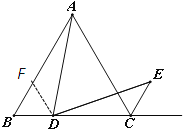
ШчЭМ1ЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЕуDЮЊBCЕФжаЕуЃЌЧвТњзуЁЯADE=60ЁуЃЌDEНЛЕШБпШ§НЧаЮЭтНЧЦНЗжЯпCEЫљдкжБЯпгкЕуEЃЌЪдЬНОПADгыDEЕФЪ§СПЙиЯЕЃЎ
ЃЈ1ЃЉаЁУїЗЂЯжЃЌЙ§ЕуDзїDF//ACЃЌНЛACгкЕуFЃЌЭЈЙ§ЙЙдьШЋЕШШ§НЧаЮЃЌОЙ§ЭЦРэТлжЄЃЌФмЙЛЪЙЮЪЬтЕУЕННтОіЃЌЧыжБНгаДГіADгыDEЕФЪ§СПЙиЯЕЃК ЃЛ
ЃЈ2ЃЉЁОРрБШЬНОПЁПШчЭМ2ЃЌЕБЕуDЪЧЯпЖЮBCЩЯЃЈГ§BЃЌCЭтЃЉШЮвтвЛЕуЪБЃЈЦфЫќЬѕМў
ВЛБфЃЉЃЌЪдВТЯыADгыDEжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ЃЈ3ЃЉЁОЭиеЙгІгУЁПЕБЕуDдкЯпЖЮBCЕФбгГЄЯпЩЯЃЌЧвТњзуCD=BCЃЈЦфЫќЬѕМўВЛБфЃЉЪБЃЌ
ЧыжБНгаДГіЁїABCгыЁїADEЕФУцЛ§жЎБШЃЎ

ЁОД№АИЁПЃЈ1ЃЉAD=DEЃЛЃЈ2ЃЉAD=DEЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКБОЬтФбЖШжаЕШЁЃжївЊПМВщбЇЩњЖдЬНОПР§згжаЕФаХЯЂНјааЙщФЩзмНсЁЃВЂФмЙЛНсКЯШ§НЧаЮЕФаджЪЪЧНтЬтЙиМќЁЃ
ЪдЬтНтЮіЃКЃЈ10ЗжЃЉ
ЃЈ1ЃЉAD=DEЃЎ
ЃЈ2ЃЉAD=DEЃЎ
жЄУїЃКШчЭМ2ЃЌЙ§ЕуDзїDF//ACЃЌНЛACгкЕуF,
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌ
ЁрAB=BCЃЌЁЯB=ЁЯACB=ЁЯABC=60ЁуЃЎ
гжЁпDF//ACЃЌ
ЁрЁЯBDF=ЁЯBFD=60Ёу
ЁрЁїBDFЪЧЕШБпШ§НЧаЮЃЌBF=BDЃЌЁЯBFD=60ЁуЃЌ
ЁрAF=CDЃЌЁЯAFD=120ЁуЃЎ
ЁпECЪЧЭтНЧЕФЦНЗжЯпЃЌ
ЁЯDCE=120Ёу=ЁЯAFDЃЎ
ЁпЁЯADCЪЧЁїABDЕФЭтНЧЃЌ
ЁрЁЯADC=ЁЯB+ЁЯFAD=60Ёу+ЁЯFADЃЎ
ЁпЁЯADC=ЁЯADE+ЁЯEDC=60Ёу+ЁЯEDCЃЌ
ЁрЁЯFAD=ЁЯEDCЃЎ
ЁрЁїAFDЁеЁїDCEЃЈASAЃЉЃЌ
ЁрAD=DEЃЛ
ЃЈ3ЃЉ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФДќжазАга3ИіТЬЧђЃЌ5ИіКьЧђКЭШєИЩАзЧђЃЌЫќУЧГ§беЩЋЭтЦфЫћЖМЯрЭЌЃЌНЋЧђНСдШЃЌДгжаШЮвтУўГівЛИіЧђЃЎ
ЃЈ1ЃЉШєДќФкга4ИіАзЧђЃЌДгжаШЮвтУўГівЛИіЧђЃЌЪЧТЬЧђЕФИХТЪЮЊЁЁ ЁЁЃЌЪЧКьЧђЕФИХТЪЮЊЁЁ ЁЁЃЌЪЧАзЧђЕФИХТЪЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉШчЙћШЮвтУўГівЛИіЧђЪЧТЬЧђЕФИХТЪЪЧ![]() ЃЌЧѓДќжагаМИИіАзЧђЃП
ЃЌЧѓДќжагаМИИіАзЧђЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБНЧзјБъЯЕжаЕФЭјИёгЩЕЅЮЛе§ЗНаЮЙЙГЩЃЌЁїABCжаЃЌAЕузјБъЮЊЃЈ2ЃЌ3ЃЉЃЌBЕузјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЌCЕузјБъЮЊЃЈ0ЃЌЉ1ЃЉЃЎ
ЃЈ1ЃЉSЁїABCЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєвдAЁЂBЁЂCМАЕуDЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЌЪддкЭМжаЛГіЫљгаDЕуЕФЮЛжУВЂЧѓГіетаЉЦНааЫФБпаЮжазюГЄЕФЖдНЧЯпГЄЮЊЁЁ ЁЁЃЌзюЖЬЕФЖдНЧЯпГЄЮЊЁЁ ЁЁЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌADЮЊЁїABCЕФжаЯпЃЌOЮЊABЩЯвЛЕуЃЌвдOЮЊдВаФЃЌAOЮЊАыОЖЕФЁбOгыABНЛгкЕуFЃЌгыBCНЛгкЕуEЃЎСЌНгAEЃЌAEЦНЗжЁЯBADЃЎ
ЃЈ1ЃЉЧѓжЄЃКBCгыЁбOЯрЧагкЕуEЃЛ
ЃЈ2ЃЉШєABЃН10ЃЌBCЃН16ЃЌЧѓЁбOЕФАыОЖЃЛ
ЃЈ3ЃЉШєADгыЁбOЕФНЛЕуЮЊЁїABCЕФжиаФЃЌдђ![]() ЕФжЕЮЊ ЃЎ
ЕФжЕЮЊ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌжБЯп
жаЃЌжБЯп![]() ЃЈ
ЃЈ![]() Чв
Чв![]() ЃЉгы
ЃЉгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() жсЃЌЧвгы
жсЃЌЧвгы![]() НЛгкЕу
НЛгкЕу![]() .
.
ЃЈ1ЃЉЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧв
ЃЌЧв![]() жсЃЌХаЖЯЫФБпаЮ
жсЃЌХаЖЯЫФБпаЮ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩ.
ЕФаЮзДЃЌВЂЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЭМЯѓЃЈелЯпOEFPMNЃЉУшЪіСЫФГЦћГЕдкааЪЛЙ§ГЬжаЫйЖШгыЪБМфЕФКЏЪ§ЙиЯЕЃЌЯТСаЫЕЗЈжаДэЮѓЕФЪЧЃЈ ЃЉ

A. Ек3ЗжЪБЦћГЕЕФЫйЖШЪЧ40ЧЇУз/ЪБ
B. Ек12ЗжЪБЦћГЕЕФЫйЖШЪЧ0ЧЇУз/ЪБ
C. ДгЕк3ЗжЕНЕк6ЗжЃЌЦћГЕааЪЛСЫ120ЧЇУз
D. ДгЕк9ЗжЕНЕк12ЗжЃЌЦћГЕЕФЫйЖШДг60ЧЇУз/ЪБМѕЩйЕН0ЧЇУз/ЪБ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯCABЕФЦНЗжЯпADгыBCЕФДЙжБЦНЗжЯпDEНЛгкЕуDЃЌDMЁЭABгкMЃЌDNЁЭACЕФбгГЄЯпгкNЃЎ
(1)ЧѓжЄЃКBM=CNЃЛ
(2)ШєAB=8ЃЌAC=4ЃЌЧѓBMЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХжаЙњДЋЭГНкШеЁАЖЫЮчНкЁБЕФСйНќЃЌЖЋЗНКьЩЬГЁОіЖЈПЊеЙЁАЛЖЖШЖЫЮчЃЌЛиРЁЙЫПЭЁБЕФШУРћДйЯњЛюЖЏЃЌЖдВПЗжЦЗХЦєезгНјааДђелЯњЪлЃЌЦфжаМзЦЗХЦєезгДђАЫелЃЌввЦЗХЦєезгДђЦпЮхелЃЌвбжЊДђелЧАЃЌТђ6КаМзЦЗХЦєезгКЭ3КаввЦЗХЦєезгаш660дЊЃЛДђелКѓЃЌТђ50КаМзЦЗХЦєезгКЭ40КаввЦЗХЦєезгашвЊ5200дЊЃЎ
ЃЈ1ЃЉДђелЧАМзЁЂввСНжжЦЗХЦєезгУПКаЗжБ№ЮЊЖрЩйдЊЃП
ЃЈ2ЃЉбєЙтОДРЯдКашЙКТђМзЦЗХЦєезг80КаЃЌввЦЗХЦєезг100КаЃЌЮЪДђелКѓЙКТђетХњєезгБШВЛДђелНкЪЁСЫЖрЩйЧЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
дкЪ§бЇПЮЩЯЃЌРЯЪІЬсГіШчЯТЮЪЬтЃК
ГпЙцзїЭМЃКзївбжЊНЧЕФНЧЦНЗжЯпЃЎ
вбжЊЃКШчЭМЃЌвбжЊ![]() .
.
ЧѓзїЃК ![]() ЕФНЧЦНЗжЯп
ЕФНЧЦНЗжЯп![]() .
.

аЁЯМЕФзїЗЈШчЯТЃК
ЃЈ1ЃЉШчЭМЃЌдкЦНУцФкШЮШЁвЛЕу![]() ЃЛ
ЃЛ
ЃЈ2ЃЉвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ ![]() ЮЊАыОЖзїдВЃЌНЛЩфЯп
ЮЊАыОЖзїдВЃЌНЛЩфЯп![]() гкЕу
гкЕу![]() ЃЌНЛЩфЯп
ЃЌНЛЩфЯп![]() гкЕу
гкЕу![]() ЃЛ
ЃЛ
ЃЈ3ЃЉСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїЩфЯп
зїЩфЯп![]() ДЙжБЯпЖЮ
ДЙжБЯпЖЮ![]() ЃЌНЛЁб
ЃЌНЛЁб![]() гкЕу
гкЕу![]() ЃЛ
ЃЛ
ЃЈ4ЃЉСЌНг![]() .
.

ЫљвдЩфЯп![]() ЮЊЫљЧѓ.
ЮЊЫљЧѓ.
РЯЪІЫЕЃКЁАаЁЯМЕФзїЗЈе§ШЗЃЎЁБ
ЧыЛиД№ЃКаЁЯМЕФзїЭМвРОнЪЧ___________________________________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com