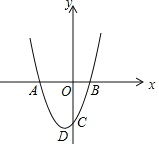
【题目】已知二次函数y＝x2+2x﹣3图象的顶点为D，与x轴交于点A、B，与y轴交于点C.
（1）求A、B、C三点的坐标；
（2）当﹣2＜x＜2时，y的取值范围是 ；
（3）判定△ACD的形状为 三角形．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】某科普小组有5名成员，身高（单位：cm）分别为：160，165，170，163，172，把身高160 cm的成员替换成一位165 cm的成员后，现科普小组成员的身高与原来相比，下列说法正确的是（ ）
A.平均数变小，方差变小B.平均数变大，方差变大
C.平均数变大，方差不变D.平均数变大，方差变小
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线
（
是常数）经过点
．
（
）求该抛物线的解析式和顶点坐标．
（
）抛物线与
轴另一交点为点
，与
轴交于点
，平行于
轴的直线
与抛物线交于点
， 
，与直线
交于点
．
①求直线
的解析式．
②若
，结合函数的图像，求
的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）（教材呈现）下图是华师版九年级上册数学教材第77页的部分内容．请根据教材提示，结合图23.4.2，写出完整的证明过程．
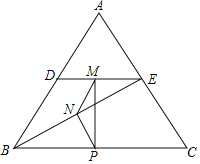
（2）（结论应用）如图，△ABC是等边三角形，点D在边AB上（点D与点A、B不重合），过点D作DE∥BC交AC于点E，连结BE，M、N、P分别为DE、BE、BC的中点，顺次连结M、N、P．
①求证：MN＝PN；
②∠MNP的大小是．
查看答案和解析>>
科目：初中数学 来源： 题型：
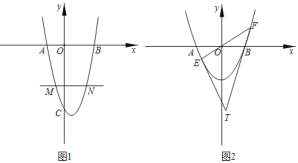
【题目】如图1，抛物线y＝a（x﹣h）2﹣9交x轴于A、B两点，交y轴于点C．
（1）若A（﹣2，0），当h＝1时，
①求抛物线的解析式．
②平行x轴的直线y＝t交抛物线于M、N点（点M在点N左侧），过M、N、C三点作⊙P．若MP⊥CP，求t值．
（2）如图2，当h＝0时，正比例函数y＝kx交抛物线于E、F两点，直线AE、BF相交于T点，求点T的运动轨迹．
查看答案和解析>>
科目：初中数学 来源： 题型：
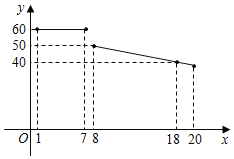
【题目】某水果超市经销一种进价为18元/kg的水果，根据以前的销售经验，该种水果的最佳销售期为20天，销售人员整理出这种水果的销售单价y（元/kg）与第x天（1≤x≤20）的函数图象如图所示，而第x天（1≤x≤20）的销售量m（kg）是x的一次函数，满足下表：
x（天） | 1 | 2 | 3 | … |
m（kg） | 20 | 24 | 28 | … |
（1）请分别写出销售单价y（元/kg）与x（天）之间及销售量m（kg）是x（天）的之间的函数关系式
（2）求在销售的第几天时，当天的利润最大，最大利润是多少？
（3）请求出试销的20天中当天的销售利润不低于1680元的天数．
查看答案和解析>>
科目：初中数学 来源： 题型：
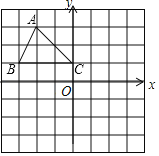
【题目】如图，在平面直角坐标系中，△ABC三个顶点都在格点上，点A，B，C的坐标分别为A（﹣2，3），B（﹣3，1），C（0，1）请解答下列问题：
（1）△ABC与△A1B1C1关于原点O成中心对称，画出△A1B1C1并直接写出点A的对应点A1的坐标；
（2）画出△ABC绕点C顺时针旋转90°后得到的△A2B2C，并求出线段AC旋转时扫过的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图
，在等腰
中，
，点E在AC上
且不与点A、C重合
，在
的外部作等腰
，使
，连接AD，分别以AB，AD为邻边作平行四边形ABFD，连接AF．
请直接写出线段AF，AE的数量关系；
将
绕点C逆时针旋转，当点E在线段BC上时，如图
，连接AE，请判断线段AF，AE的数量关系，并证明你的结论；
若
，
，在图的基础上将绕点C继续逆时针旋转一周的过程中，当平行四边形ABFD为菱形时，直接写出线段AE的长度．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
