
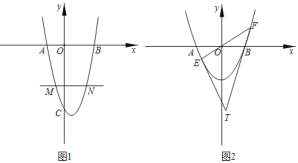
【题目】如图1,抛物线y=a(x﹣h)2﹣9交x轴于A、B两点,交y轴于点C.
(1)若A(﹣2,0),当h=1时,
①求抛物线的解析式.
②平行x轴的直线y=t交抛物线于M、N点(点M在点N左侧),过M、N、C三点作⊙P.若MP⊥CP,求t值.
(2)如图2,当h=0时,正比例函数y=kx交抛物线于E、F两点,直线AE、BF相交于T点,求点T的运动轨迹.
【答案】(1)①![]() ;②
;②![]() ;(2)T在直线
;(2)T在直线![]() 上运动.
上运动.
【解析】
(1)①由已知可得![]() ,将A(-2,0)代入抛物线解析式可得
,将A(-2,0)代入抛物线解析式可得![]() ;
;
②由已知可得P点在MN的垂直平分线上,P点在抛物线对称轴x=1上,设![]()
![]() ,则△PCM是等腰直角三角形,所以
,则△PCM是等腰直角三角形,所以![]() ,
,![]() ,∠MNC=
,∠MNC=![]() ∠MPC=45°,设MN与y轴的交点为H,则HN=HC,所以
∠MPC=45°,设MN与y轴的交点为H,则HN=HC,所以![]() ,令
,令![]() ,可得
,可得![]() ,
,![]() ,求出t即可;
,求出t即可;
(2)由已知可得y=ax2-9,设A(-s,0),B(s,0),所以as2=9,AE的直线解析式为y=k1x+k1s与抛物线相交可得![]() ,
,![]() ,直线BF的解析式为y=k2x-k2s与抛物线相交可得
,直线BF的解析式为y=k2x-k2s与抛物线相交可得![]() ,
,![]() ,直线EF的解析式为y=kx与抛物线相交可得
,直线EF的解析式为y=kx与抛物线相交可得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,直线AE与直线BF相交可得T
,直线AE与直线BF相交可得T![]() ,
,![]() ,求得T
,求得T![]() ,
,![]() ,可得T在直线y=18上运动.
,可得T在直线y=18上运动.
(1)①将h=1,A(﹣2,0)代入![]() 得:
得:
解得:![]() ,
,
∴![]()
即:![]() ;
;
②∵M、N、C三点作⊙P,
∴P点在MN的垂直平分线上,
∴P点在抛物线对称轴x=1上,
如图,MN交y轴和抛物线对称轴![]() 于分别为点H和G,过点C作抛物线对称轴x=1的垂线垂足为D,连接NC,
于分别为点H和G,过点C作抛物线对称轴x=1的垂线垂足为D,连接NC,
∵MN平行x轴,
∴四边形CDGH为矩形,
∴DG=HC,GH=CD=1,
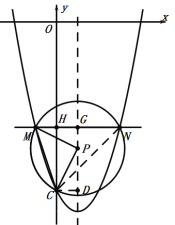
∵PM=PC,PM⊥PC,
∴△PCM是等腰直角三角形,∠MPC=∠MGP=∠PDC=![]() ,
,
∵∠MPG+∠CPD=∠PCD+∠CPD =![]() ,
,
∴∠MPG=∠PCD,
在![]() 和
和![]() 中,
中, ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴m=﹣t﹣6,
∴∠MNC=![]() ∠MPC=45°,
∠MPC=45°,
∴HN=HC,
∴![]() ,
,
∴![]() ,
,
令![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (舍)或
(舍)或![]() ,
,
∴![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
设![]() ,
,
∴![]() ,
,
∴AE的直线解析式为![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
直线BF的解析式为![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵直线EF的解析式为![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵as2=9,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵ ,
,
∴T![]() ,
,![]() ),
),
∵![]() ,
,
∴T![]() ,
,![]() ),
),
∴T在直线y=18上运动.


科目:初中数学 来源: 题型:
【题目】如图,认真观察下面这些算式,并结合你发现的规律,完成下列问题:
算式①![]() ,
,
算式②![]() ,
,
算式③![]() ,
,
算式④![]() ,
,
…
(1)请写出:算式③______;算式④______;
(2)上述算式的规律可以用文字概括为:“两个连续奇数的平方差能被8整除”,如果设两个连续奇数分别为![]() 和
和![]() (
(![]() 为整数),请说明这个规律是成立的;
为整数),请说明这个规律是成立的;
(3)你认为“两个连续偶数的平方差能被8整除”这个说法是否也成立呢?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图所示,已知原阶梯式扶梯AB长为10m,坡角∠ABD=30°;改造后斜坡式自动扶梯的坡角∠ACB=9°,请计算改造后的斜坡AC的长度,(结果精确到0.01(sin9°≈0.156,cos9°≈0.988,tan9°≈0.158)
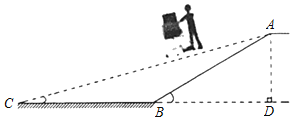
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+2x﹣3图象的顶点为D,与x轴交于点A、B,与y轴交于点C.
(1)求A、B、C三点的坐标;
(2)当﹣2<x<2时,y的取值范围是 ;
(3)判定△ACD的形状为 三角形.
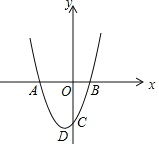
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点的坐标分别为A(2,2),B(1,0),C(3,1).

(1)画出△ABC关于x轴对称的△A1BC1,写出点C1的坐标为 ;
(2)画出△ABC绕原点O逆时针旋转90°的△A2B1C2,写出点C2的坐标为 ;
(3)在(1),(2)的基础上,图中的△A1BC1、△A2B1C2关于点 中心对称;
(4)若以点D、A、C、B为顶点的四边形为菱形,直接写出点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1:4,求边CD的长.
(2)如图2,在(1)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度.
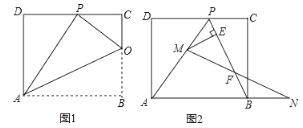
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是抛物线上的动点,且满足S△PAO=2S△PCO,求出P点的坐标;
(3)连接BC,点E是x轴一动点,点F是抛物线上一动点,若以B、C、E、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.
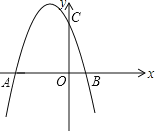
查看答案和解析>>
科目:初中数学 来源: 题型:
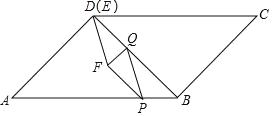
【题目】如图,BD是ABCD的对角线,AD⊥BD,AB=2![]() cm,∠A=45°.动点P从点B出发,以
cm,∠A=45°.动点P从点B出发,以![]() cm/s的速度沿BA运动到终点A,同时动点Q从点D出发,以2cm/s的速度沿折线DB﹣BC向终点C运动,当一点到达终点时另一点也停止运动.过点Q作QE⊥AD,交射线AD于点E,连接PQ,以PQ与EQ为边作PQEF.设点P的运动时间为t(s),PQEF与ABCD重叠部分图形的面积为S(cm2).
cm/s的速度沿BA运动到终点A,同时动点Q从点D出发,以2cm/s的速度沿折线DB﹣BC向终点C运动,当一点到达终点时另一点也停止运动.过点Q作QE⊥AD,交射线AD于点E,连接PQ,以PQ与EQ为边作PQEF.设点P的运动时间为t(s),PQEF与ABCD重叠部分图形的面积为S(cm2).
(1)AP= cm(用含的代数式表示);
(2)当点F落在边AD上时,求t的值:
(3)求S与t之间的函数关系式;
(4)连接FQ,当FQ所在的直线将ABCD分成面积相等的两部分时,直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com