
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
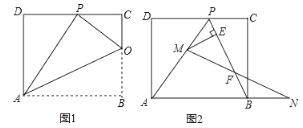
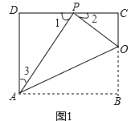
(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1:4,求边CD的长.
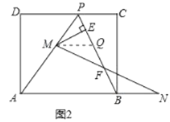
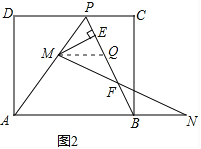
(2)如图2,在(1)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度.
【答案】(1)10;(2)![]() .
.
【解析】
(1)先证出∠C=∠D=90°,再根据∠1+∠3=90°,∠1+∠2=90°,得出∠2=∠3,即可证出△OCP∽△PDA;根据△OCP与△PDA的面积比为1:4,得出CP=![]() AD=4,设OP=x,则CO=8﹣x,由勾股定理得 x2=(8﹣x)2+42,求出x,最后根据AB=2OP即可求出边AB的长;
AD=4,设OP=x,则CO=8﹣x,由勾股定理得 x2=(8﹣x)2+42,求出x,最后根据AB=2OP即可求出边AB的长;
(2)作MQ∥AN,交PB于点Q,求出MP=MQ,BN=QM,得出MP=MQ,根据ME⊥PQ,得出EQ=![]() PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=
PQ,根据∠QMF=∠BNF,证出△MFQ≌△NFB,得出QF=![]() QB,再求出EF=
QB,再求出EF=![]() PB,由(1)中的结论求出PB=
PB,由(1)中的结论求出PB=![]() ,最后代入EF=
,最后代入EF=![]() PB即可得出线段EF的长度不变
PB即可得出线段EF的长度不变
(1)如图1,∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴∠1+∠3=90°,
∵由折叠可得∠APO=∠B=90°,
∴∠1+∠2=90°,∴∠2=∠3,
又∵∠D=∠C,
∴△OCP∽△PDA;
∵△OCP与△PDA的面积比为1:4,
∴![]() ,∴ CP=
,∴ CP=![]() AD=4
AD=4
设OP=x,则CO=8﹣x,
在Rt△PCO中,∠C=90°,由勾股定理得 x2=(8﹣x)2+42,
解得:x=5,∴AB=AP=2OP=10,∴边CD的长为10;
(2)作MQ∥AN,交PB于点Q,如图2,
∵AP=AB,MQ∥AN,
∴∠APB=∠ABP=∠MQP.∴MP=MQ,∵BN=PM,
∴BN=QM.
∵MP=MQ,ME⊥PQ,
∴EQ=PQ.∵MQ∥AN,∴∠QMF=∠BNF,
∴△MFQ≌△NFB.
∴QF=FB,∴EF=EQ+QF=![]() (PQ+QB)=
(PQ+QB)=![]() PB,
PB,
由(1)中的结论可得:PC=4,BC=8,∠C=90°,
∴PB=![]() ,∴EF=
,∴EF=![]() PB=2
PB=2![]() ,
,
∴在(1)的条件下,当点M、N在移动过程中,线段EF的长度不变,它的长度为2![]() .
.


科目:初中数学 来源: 题型:
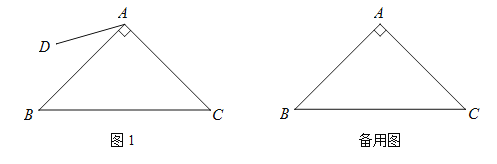
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)请根据题意补全图1;
(2)猜测BD和CE的数量关系并证明;
(3)作射线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() 是常数)经过点
是常数)经过点![]() .
.
(![]() )求该抛物线的解析式和顶点坐标.
)求该抛物线的解析式和顶点坐标.
(![]() )抛物线与
)抛物线与![]() 轴另一交点为点
轴另一交点为点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,平行于
,平行于![]() 轴的直线
轴的直线![]() 与抛物线交于点
与抛物线交于点![]() ,
, ![]() ,与直线
,与直线![]() 交于点
交于点![]() .
.
①求直线![]() 的解析式.
的解析式.
②若![]() ,结合函数的图像,求
,结合函数的图像,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
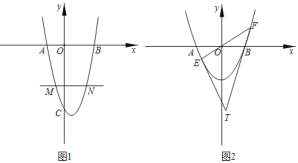
【题目】如图1,抛物线y=a(x﹣h)2﹣9交x轴于A、B两点,交y轴于点C.
(1)若A(﹣2,0),当h=1时,
①求抛物线的解析式.
②平行x轴的直线y=t交抛物线于M、N点(点M在点N左侧),过M、N、C三点作⊙P.若MP⊥CP,求t值.
(2)如图2,当h=0时,正比例函数y=kx交抛物线于E、F两点,直线AE、BF相交于T点,求点T的运动轨迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
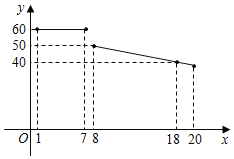
【题目】某水果超市经销一种进价为18元/kg的水果,根据以前的销售经验,该种水果的最佳销售期为20天,销售人员整理出这种水果的销售单价y(元/kg)与第x天(1≤x≤20)的函数图象如图所示,而第x天(1≤x≤20)的销售量m(kg)是x的一次函数,满足下表:
x(天) | 1 | 2 | 3 | … |
m(kg) | 20 | 24 | 28 | … |
(1)请分别写出销售单价y(元/kg)与x(天)之间及销售量m(kg)是x(天)的之间的函数关系式
(2)求在销售的第几天时,当天的利润最大,最大利润是多少?
(3)请求出试销的20天中当天的销售利润不低于1680元的天数.
查看答案和解析>>
科目:初中数学 来源: 题型:
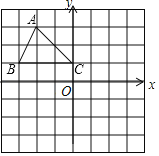
【题目】如图,在平面直角坐标系中,△ABC三个顶点都在格点上,点A,B,C的坐标分别为A(﹣2,3),B(﹣3,1),C(0,1)请解答下列问题:
(1)△ABC与△A1B1C1关于原点O成中心对称,画出△A1B1C1并直接写出点A的对应点A1的坐标;
(2)画出△ABC绕点C顺时针旋转90°后得到的△A2B2C,并求出线段AC旋转时扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C = 90°,点O是斜边AB上一定点,到点O的距离等于OB的所有点组成图形W,图形W与AB,BC分别交于点D,E,连接AE,DE,∠AED=∠B.

(1)判断图形W与AE所在直线的公共点个数,并证明.
(2)若![]() ,
,![]() ,求OB.
,求OB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com