
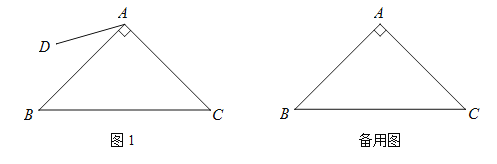
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=AC.在平面内任取一点D,连结AD(AD<AB),将线段AD绕点A逆时针旋转90°,得到线段AE,连结DE,CE,BD.
(1)请根据题意补全图1;
(2)猜测BD和CE的数量关系并证明;
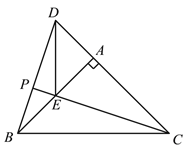
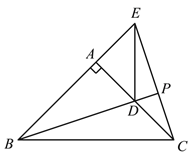
(3)作射线BD,CE交于点P,把△ADE绕点A旋转,当∠EAC=90°,AB=2,AD=1时,补全图形,直接写出PB的长.
【答案】(1)答案见解析;(2)BD=CE;(3)PB的长是![]() 或
或![]() .
.
【解析】试题分析:(1)根据题意画出图形即可;(2)根据“SAS”证明△ABD≌△ACE,从而可得BD=CE;(3)①根据“SAS”可证△ABD≌△ACE,从而得到∠ABD=∠ACE,再由两角对应相等的两个三角形相似可证△ACD∽△PBE,列比例方程可求出PB的长;②与①类似,先求出PD的长,再把PD和BD相加.
解:(1)如图
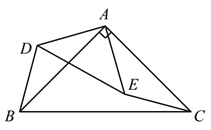
(2)BD和CE的数量是:BD=CE ;
∵∠DAB+∠BAE=∠CAE+∠BAE=90°,∴∠DAB=∠CAE.
∵AD=AE,AB=AC,∴△ABD≌△ACE,∴BD=CE.
(3)①CE=![]() .
.
∵△ABD≌△ACE, ∴∠ABD=∠ACE,
∴△ACD∽△PBE,
![]() ,
,
∴![]() ;
;
②∵△ABD∽△PDC,
![]() ,
,
∴![]() ;
;
∴PB=PD+BD=![]() .
.
∴PB的长是![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
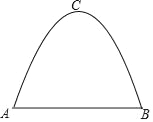
【题目】一条单车道的抛物线形隧道如图所示.隧道中公路的宽度AB=8m,隧道的最高点C到公路的距离为6m.
(1)建立适当的平面直角坐标系,求抛物线的表达式;
(2)现有一辆货车的高度是4.4m,货车的宽度是2m,为了保证安全,车顶距离隧道顶部至少0.5m,通过计算说明这辆货车能否安全通过这条隧道.
查看答案和解析>>
科目:初中数学 来源: 题型:
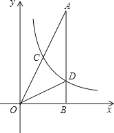
【题目】如图,在Rt△AOB中,∠ABO=90°,OB=4,AB=8,且反比例函数y=![]() 在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
在第一象限内的图象分别交OA,AB于点C和点D,连结OD,△BOD的面积是4.
(1)求反比例函数解析式;
(2)将△AOB沿x轴向左运动,运动速度是每秒钟3个单位长度,求△AOB与反比例函数图象没有交点时,运动时间t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,认真观察下面这些算式,并结合你发现的规律,完成下列问题:
算式①![]() ,
,
算式②![]() ,
,
算式③![]() ,
,
算式④![]() ,
,
…
(1)请写出:算式③______;算式④______;
(2)上述算式的规律可以用文字概括为:“两个连续奇数的平方差能被8整除”,如果设两个连续奇数分别为![]() 和
和![]() (
(![]() 为整数),请说明这个规律是成立的;
为整数),请说明这个规律是成立的;
(3)你认为“两个连续偶数的平方差能被8整除”这个说法是否也成立呢?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数
的图象与y轴交于点A,点B(-1,n)是该函数图象与反比例函数![]() (k≠0)图象在第二象限内的交点.
(k≠0)图象在第二象限内的交点.
(1)求点B的坐标及k的值;
(2)试在x轴上确定点C,使AC=AB,请直接写出点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
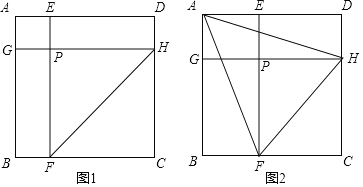
【题目】如图,边长为a的正方形ABCD被两条与边平行的线段EF、GH分割成四个小矩形,EF与GH交于点P,连接AF、AH、FH.
(1)如图1,若a=1,AE=AG=![]() ,求FH的值;
,求FH的值;
(2)如图2,若∠FAH=45°,证明:AG+AE=FH;
(3)若Rt△GBF的周长l=a,求矩形EPHD的面积S与l的关系(只写结果,不写过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
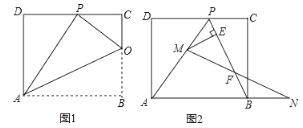
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.
(1)如图1,已知折痕与边BC交于点O,连接AP、OP、OA.若△OCP与△PDA的面积比为1:4,求边CD的长.
(2)如图2,在(1)的条件下,擦去折痕AO、线段OP,连接BP.动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连接MN交PB于点F,作ME⊥BP于点E.试问当动点M、N在移动的过程中,线段EF的长度是否发生变化?若变化,说明变化规律.若不变,求出线段EF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com