
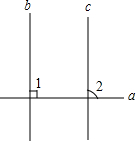
 如图,已知直线b∥c,a⊥b,求证:a⊥c.
如图,已知直线b∥c,a⊥b,求证:a⊥c. 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:
 如图,直线l1∥l2∥l3,点A、B、C分别在直线l1、l2、l3上.若∠1=70°,∠2=50°,则∠ABC等于( )
如图,直线l1∥l2∥l3,点A、B、C分别在直线l1、l2、l3上.若∠1=70°,∠2=50°,则∠ABC等于( )| A、95° | B、100° |
| C、110° | D、120° |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
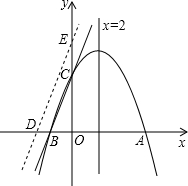 如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中A点的坐标为(5,0).
如图,对称轴为直线x=2的抛物线y=ax2+bx+c(a≠0)与x轴相交于A、B两点,其中A点的坐标为(5,0).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
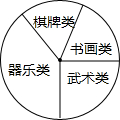 某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数:
某校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数:| 类别 | 频数(人数) | 频率 |
| 武术类 | 25 | 0.25 |
| 书画类 | a | 0.20 |
| 棋牌类 | 15 | b |
| 器乐类 | 40 | 0.40 |
| 合计 | 1.00 |
查看答案和解析>>
科目:初中数学 来源: 题型:
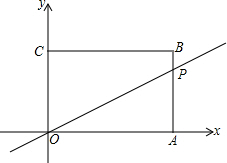 如图:矩形OABC中A(4,0),C(0,3).动点P从A→B→C以每秒1个单位的速度运动.记OP在矩形中扫过的面积为S,运动时间为t
如图:矩形OABC中A(4,0),C(0,3).动点P从A→B→C以每秒1个单位的速度运动.记OP在矩形中扫过的面积为S,运动时间为t查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com