
分析 先将等式的左边根据完全平方公式展开,再根据等式的恒等原理就可以求出结论.
解答 解:∵(x+m)2=x2+2mx+m2,
∴x2+2mx+m2=x2+nx+36,
∴$\left\{\begin{array}{l}2m=n\\{m}^{2}=36\end{array}\right.$,
解得$\left\{\begin{array}{l}{m}_{1}=6\\{n}_{1}=12\end{array}\right.$,$\left\{\begin{array}{l}{m}_{2}=-6\\{n}_{2}=-12\end{array}\right.$.
故答案为:±6,±12.
点评 本题考查的是完全平方公式,熟知熟记完全平方公式是解答此题的关键.


 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:填空题
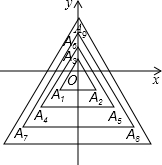 如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们
如图,所有正三角形的一边平行于x轴,一顶点在y轴上,从内到外,它们查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是2012年10月份的日历表,任意圈出一竖列上相邻的三个数.请你运用方程思想来研究,发现这三个数的和不可能是( )
如图是2012年10月份的日历表,任意圈出一竖列上相邻的三个数.请你运用方程思想来研究,发现这三个数的和不可能是( )| A. | 69 | B. | 54 | C. | 27 | D. | 40 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com