练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    先化简，再求值：（1+x）（1-x）-x（2-x），其中x=-3．
    考点：整式的混合运算—化简求值
    专题：
    分析：先算乘法，再合并同类项，最后代入求出即可．
    解答：解：（1+x）（1-x）-x（2-x）
    =1-x2-2x+x2
    =1-2x，
    当x=-3时，原式=1-2×（-3）=7．
    点评：本题考查了整式的混合运算和求值的应用，主要考查学生的计算能力和化简能力，难度适中．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，已知点B、C、E在一直线上，且∠1=∠B，那么
     
    ∥
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

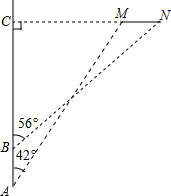    钓鱼岛自古就是中国的领土，中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视监测．一日，中国一艘海监船从A点沿正北方向巡航，其航线距钓鱼岛（设M，N为该岛的东西两端点）最近距离为14.4km（即MC=14.4km）．在A点测得岛屿的西端点M在点A的北偏东42°方向；航行4km后到达B点，测得岛屿的东端点N在点B的北偏东56°方向，（其中N，M，C在同一条直线上），求钓鱼岛东西两端点MN之间的距离（结果精确到0.1km）．（参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90，sin56°≈0.83，cos56°≈0.56，tan56°≈1.48）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    把经过点（-1，1）和（1，3）的直线向右移动2个单位后过点（3，a），则a的值为（　　）
    A、1B、2C、3D、4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：（
    		2
    -
    		3
    ）2015•（
    		2
    +
    		3
    ）2015-（
    		18
    -
    		8
    ）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    按照如图所示的操作步骤，若输入x的值为1，则输出的值为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，AB是⊙O的直径，CD切⊙O于D，CF⊥AB于F，若tan∠A=2，求sin∠DCF的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    阅读下面材料：
    课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB=5，AC=3，求BC边上的中线AD的取值范围．
    小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使DE=AD，再连接BE，相当于把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，即可得到AD的取值范围．请你写出AD的取值范围
     
    ；
    小明小组的感悟：解题时，可以通过构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形中．
    请你解决以下问题：
    （1）如图2，在△ABC中，D是BC边上的中点，ED⊥DF，DE交AB于点E，DF交AC于点F，连接EF．
    ①求证：BE+CF＞EF；
    ②若∠A=90°，请直接写出线段BE、CF、EF之间的数量关系为
     
    ．
    （2）如图3，在四边形ABDC中，∠B+∠C=180°，DB=DC，∠BDC=120°，以D为顶点作一个60°的角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【问题情境】
    徐老师给爱好学习的小敏和小捷提出这样一个问题：
    如图1，△ABC中，∠B=2∠C，AD是∠BAC的平分线．求证：AB+BD=AC
    小敏的证明思路是：在AC上截取AE=AB，连接DE．（如图2）…
    小捷的证明思路是：延长CB至点E，使BE=AB，连接AE． 可以证得：AE=DE（如图3）…
    请你任意选择一种思路继续完成下一步的证明．
    【变式探究】
    “AD是∠BAC的平分线”改成“AD是BC边上的高”，其它条件不变．（如图4），AB+BD=AC成立吗？若成立，请证明；若不成立，写出你的正确结论，并说明理由．
    【迁移拓展】
    △ABC中，∠B=2∠C． 求证：AC2=AB2+AB•BC． （如图5）

    查看答案和解析>>

    同步练习册答案