Question

【题目】一次函数y=kx+b的图象与x、y轴分别交于点A（2，0），B（0，4）．

（1）求该函数的解析式；
（2）O为坐标原点，设OA、AB的中点分别为C、D，P为OB上一动点，求PC+PD的最小值，并求取得最小值时P点的坐标．

Answer 1

【答案】
（1）

解：将点A、B的坐标代入y=kx+b得：

0=2k+b，4=b，

∴k=﹣2，b=4，

∴解析式为：y=﹣2x+4

（2）

解：

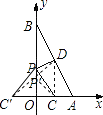
设点C关于点O的对称点为C′，连接C′D交OB于P′，连接P′C，则PC=PC′，

∴PC+PD=PC′+PD=C′D，即PC+PD的最小值是C′D．

连接CD，在Rt△DCC′中，C′D= =2 ，即PC′+PD的最小值为2 ，

∵OA、AB的中点分别为C、D，

∴CD是△OBA的中位线，

∴OP∥CD，CD= OB=2，

∵C′O=OC，

∴OP是△C′CD的中位线，

∴OP= CD=1，

∴点P的坐标为（0，1）．

【解析】（1）将点A、B的坐标代入y=kx+b并计算得k=﹣2，b=4．求出解析式为：y=﹣2x+4；（2）设点C关于点O的对称点为C′，连接C′D交OB于P，则PC=PC′，PC+PD=PC′+PD=C′D，即PC+PD的最小值是C′D．连接CD，在Rt△DCC′中，由勾股定理求得C′D的值，由OP是△C′CD的中位线而求得点P的坐标．
【考点精析】本题主要考查了一次函数的性质的相关知识点，需要掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小才能正确解答此题．