
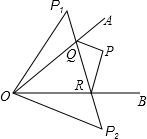
 如图所示,∠AOB=45°,角内有一点P,P1、P2分别是点P关于两边OA和OB的对称点,连P1P2与角两边交于Q、R.
如图所示,∠AOB=45°,角内有一点P,P1、P2分别是点P关于两边OA和OB的对称点,连P1P2与角两边交于Q、R.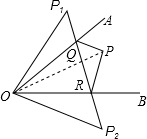 解:(1)∵P1、P2分别是点P关于两边OA和OB的对称点,
解:(1)∵P1、P2分别是点P关于两边OA和OB的对称点,

科目:初中数学 来源: 题型:
| A、-2y的系数是-2,次数是1 |
| B、单项式ab2的系数是1,次数是2 |
| C、2x-3是一次二项式 |
| D、3x2+xy-4是二次三项式 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 在一边靠墙的空地上,用砖墙围成三格的矩形场地,已知砖墙在地面上占地总长度160m,问分隔墙在地面上的长度x为多少时所围场地总面积最大?并求这个最大面积.
在一边靠墙的空地上,用砖墙围成三格的矩形场地,已知砖墙在地面上占地总长度160m,问分隔墙在地面上的长度x为多少时所围场地总面积最大?并求这个最大面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com