
 如图,在正方形ABCD中,E、F分别为BC、AB上的点,且∠FED=90°,∠DFE=60°,若正方形边长为1,求△DEF的面积.
如图,在正方形ABCD中,E、F分别为BC、AB上的点,且∠FED=90°,∠DFE=60°,若正方形边长为1,求△DEF的面积.| EF |
| DE |
| ||
| 3 |
| EF |
| DE |
| ||
| 3 |
| BE |
| CD |
| EF |
| DE |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
7-2
| ||
| 3 |
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 6 |
7-2
| ||
| 3 |
7
| ||
| 18 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
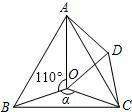 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.查看答案和解析>>
科目:初中数学 来源: 题型:
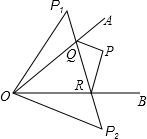 如图所示,∠AOB=45°,角内有一点P,P1、P2分别是点P关于两边OA和OB的对称点,连P1P2与角两边交于Q、R.
如图所示,∠AOB=45°,角内有一点P,P1、P2分别是点P关于两边OA和OB的对称点,连P1P2与角两边交于Q、R.查看答案和解析>>
科目:初中数学 来源: 题型:
 操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a、b、c(如图①),分别用4张这样的直角三角形纸片拼成如图②③的形状,图②中的两个小正方形的面积S2、S3与图③中小正方形的面积S1有什么关系?你能得到a、b、c之间有什么关系?
操作:剪若干个大小形状完全相同的直角三角形,三边长分别记为a、b、c(如图①),分别用4张这样的直角三角形纸片拼成如图②③的形状,图②中的两个小正方形的面积S2、S3与图③中小正方形的面积S1有什么关系?你能得到a、b、c之间有什么关系?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com