
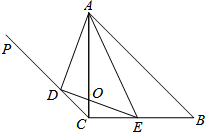
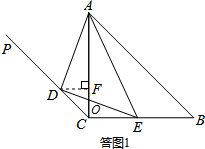
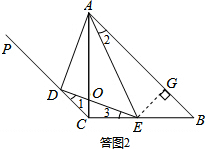
 已知:如图,在等腰直角△ABC中,AC=BC,斜边AB的长为4,过点C作射线CP∥AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.
已知:如图,在等腰直角△ABC中,AC=BC,斜边AB的长为4,过点C作射线CP∥AB,D为射线CP上一点,E在边BC上(不与B、C重合),且∠DAE=45°,AC与DE交于点O.| AD |
| AE |
| AC |
| AB |
| AD |
| AC |
| AE |
| AB |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| ||
| 2 |
| DF |
| AF |
| ||||||
2
|
| x |
| 4-x |
| x |
| 4-x |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
 中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固翼飞机的航空母舰,满载排水量为67500吨,这个数据67500用科学记数法表示为6.75×10n(n是正整数),则n的值等于
中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固翼飞机的航空母舰,满载排水量为67500吨,这个数据67500用科学记数法表示为6.75×10n(n是正整数),则n的值等于查看答案和解析>>
科目:初中数学 来源: 题型:
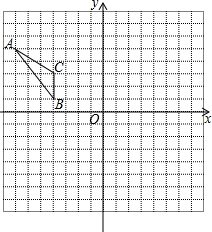 如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.
如图,△ABC在平面直角坐标系中,将△ABC向右平移5个单位得到△A1B1C1,再将△A1B1C1绕点B1顺时针旋转90°得到△A2B2C2.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com