
【题目】如图,在等腰△ABC中,点D、E分别是两腰AC、BC上的点,连接AE、BD相交于点O,∠1=∠2. 
(1)求证:OD=OE;
(2)求证:四边形ABED是等腰梯形;
(3)若AB=3DE,△DCE的面积为2,求四边形ABED的面积.
【答案】
(1)证明:如图,∵△ABC是等腰三角形,
∴AC=BC,
∴∠BAD=∠ABE,
又∵AB=BA、∠2=∠1,
∴△ABD≌△BAE(ASA),
∴BD=AE,
又∵∠1=∠2,
∴OA=OB,
∴BD﹣OB=AE﹣OA,
即:OD=OE
(2)证明:由①得OD=OE,
∴∠DOE=∠BOA,
![]() ,
,
∴△DOE∽△BOA,
∴∠EDO=∠ABO,
∴DE∥AB,
又∵∠DAB=∠EBA,
∴四边形ABEO为等腰梯形
(3)解:由(2)可知:DE∥AB,
∴∠CED=∠CBA,∠CDE=∠CAB,
∴△DCE∽△ACB(AA),
∴ ![]() =(
=( ![]() )2,
)2,
即 ![]() =(
=( ![]() )2=
)2= ![]() .
.
∴S△ACB=18,
∴S四边形ABED=S△ACB﹣S△DCE=18﹣2=16
【解析】(1)如图,由△ABC是等腰三角形,得到∠BAD=∠ABE,然后利用已知条件证明△ABD≌△BAE,由全等三角形的性质得到BD=AE,又由∠1=∠2得到OA=OB,由此即可证明OD=OE;(2)由(1)得OD=OE根据等腰三角形的性质得到∠OED=∠ODE,根据三角形的内角和得到∠OED= ![]() (180°﹣∠DOE),∠1=
(180°﹣∠DOE),∠1= ![]() (180°﹣∠AOB),而∠DOE=∠AOB,所以得到∠1=∠OED,然后利用平行线的判定得到DE∥AB,最后证明AD与BE不平行,这样就可以证明梯形ABED是等腰梯形;(3)由(2)可知DE∥AB,然后得到△DCE∽△ACB,接着利用相似三角形的性质即可求出S△ACB , 然后就可以求出S四边形ABED .
(180°﹣∠AOB),而∠DOE=∠AOB,所以得到∠1=∠OED,然后利用平行线的判定得到DE∥AB,最后证明AD与BE不平行,这样就可以证明梯形ABED是等腰梯形;(3)由(2)可知DE∥AB,然后得到△DCE∽△ACB,接着利用相似三角形的性质即可求出S△ACB , 然后就可以求出S四边形ABED .
【考点精析】通过灵活运用等腰三角形的性质和等腰梯形的判定,掌握等腰三角形的两个底角相等(简称:等边对等角);两腰相等的梯形是等腰梯形;同一底上的两个角相等的梯形是等腰梯形;两条对角线相等的梯形是等腰梯形即可以解答此题.


科目:初中数学 来源: 题型:
【题目】在矩形纸片ABCD中,AB=6,BC=8.
(1)如图①,将矩形纸片沿AN折叠,点B落在对角线AC上的点E处,求BN的长;
(2)如图②,点M为AB上一点,将△BCM沿CM翻折至△ECM,ME与AD相交于点G,CE与AD相交于点F,且AG=GE,求BM的长;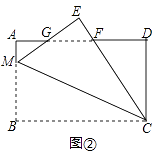
(3)如图③,将矩形纸片ABCD折叠,使顶点B落在AD边上的点E处,折痕所在直线同时经过AB、BC(包括端点),设DE=x,请直接写出x的取值范围: . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF. 
(1)求证:四边形AECF是平行四边形;
(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O1、⊙O2相内切于点A,其半径分别是8和4,将⊙O2沿直线O1O2平移至两圆相外切时,则点O2移动的长度是( ) 
A.4
B.8
C.16
D.8或16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于( )
A.![]()
B.![]()
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求此切线长;
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(﹣4,6),(﹣1,4).
(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)请在y轴上求作一点P,使△PB1C的周长最小,并写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足OAOB=OP2 , 我们就把∠APB叫做∠MON的智慧角.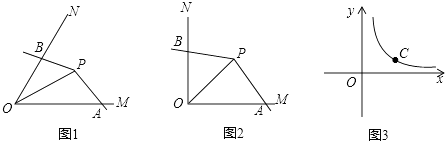
(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°.求证:∠APB是∠MON的智慧角.
(2)如图1,已知∠MON=α(0°<α<90°),OP=2.若∠APB是∠MON的智慧角,连结AB,用含α的式子分别表示∠APB的度数和△AOB的面积.
(3)如图3,C是函数y= ![]() (x>0)图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
(x>0)图象上的一个动点,过C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com