
����Ŀ��ijУ������չ��������������������������������������ܲ������˶���Ŀ��Ϊ�˽�ѧ����ϲ����һ����Ŀ��ͯ�������ȡ�˲���ѧ�����е��飬�����������µ�����ͳ��ͼ������ͳ��ͼ��������Ϣδ������
��1�����α������ѧ������Ϊ����������ͳ��ͼ�����ܲ������Ե�Բ�Ľ�Ϊ���ȣ�
��2����ȫ����ͳ��ͼ��
��3����У����1200��ѧ���������ȫУ��ϲ���������������ϲ���������������٣�

���𰸡���1��40��27����2��������;��3��90�ˣ�
��������
��1����ϲ��������������������ռ�İٷֱȼ�����ñ��������������������������������ռ�İٷֱȼ������ϲ���������������������ȥ������С��������������ϲ���ܲ�������������360����ԡ��ܲ���������ռ�������ɵã�
��2������������������ȫ����ͳ��ͼ��
��3���������������弴��ȷ����ϲ���������������ϲ���������������٣�
�⣺��1���۲�����ͳ��ͼ������ͳ��ͼ֪��ϲ����������10�ˣ�ռ25%��
����������10��25%=40�ˣ�
����ϲ���������40��30%=12�ˣ�
ϲ���ܲ�����40��10��15��12=3�ˣ�
������ͳ��ͼ�����ܲ������Ե�Բ�Ľ�Ϊ360����![]() =27�㣬
=27�㣬
�ʴ�Ϊ��40��27��
��2������ͳ��ͼ����Ϊ��

��3��ȫУ��ϲ���������������ϲ�������������1200��![]() =90�ˣ�
=90�ˣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һö���ػ���Ӿ��״�վC��5km�ĵ���O�����䣬����������A��Bʱ�����״�վC����õ�A��B�����Ƿֱ�Ϊ34�㣬45�������е�O��A��B��ͬһ��ֱ���ϣ���A��B�����ľ��루�����ȷ��0.1km����
���ο����ݣ�sin34��=0.56��cos34��=0.83��tan34��=0.67����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB��90������A��30�����Ե�CΪԲ�ģ�CB��Ϊ�뾶��������AB�ڵ�D���ٷֱ��Ե�B�͵�DΪԲ�ģ�����![]() �ij�Ϊ�뾶�����������ཻ�ڵ�E��������CE��AB�ڵ�F����AF��6����BC�ij�Ϊ_____��
�ij�Ϊ�뾶�����������ཻ�ڵ�E��������CE��AB�ڵ�F����AF��6����BC�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ϰ���ϣ�С���������¿��һ����Ŀ��ԭ���⣩�ͺ���ѧϰС���ͬѧ�ǽ�����
��ͼ1����֪��ABC����ACB��90������ABC��45�����ֱ���AB��BCΪ����������ABD���BCE����DA��DB��EB��EC����ADB����BEC��90��������DE��AB�ڵ�F��̽���߶�DF��EF��������ϵ��
С��ͬѧ��˼·�ǣ�����D��DG��AB�ڵ�G������ȫ�������Σ�ͨ������ʹ����ý⣮
С��ͬѧ˵��������һ�����Ƶ���Ŀ����ͬ���ǡ�ABC��30������ADB����BEC��60����
����ο�С��ͬѧ��˼·��̽��������������⣺
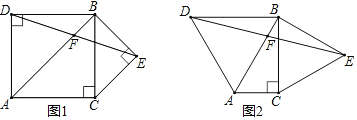
��1��д��ԭ������DF��EF��������ϵΪ�� ��
��2����ͼ2������ABC��30������ADB����BEC��60����ԭ�����е������������䣬���ڣ�1���еõ��Ľ����Ƿ����仯����д����IJ��벢����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�BE��CD�ֱ�Ϊ���ƽ�����ҽ��ڵ�O.
(1)����A��60��ʱ�����BOC�Ķ�����
(2)����A��100��ʱ�����BOC�Ķ�����
(3)����A����ʱ�����BOC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ����D��AC���е㣬ֱ��
����D��AC���е㣬ֱ��![]() �����߷ֱ�AB��BC�ڵ�E��F���������½��ۣ���
�����߷ֱ�AB��BC�ڵ�E��F���������½��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ����
����![]() �ǵ���ֱ��������. ��
�ǵ���ֱ��������. ��![]() ��
��![]() ���ƶ���D��תʱ(��E�����A��B�غ�)����������ʼ�ճ�������____________��.
���ƶ���D��תʱ(��E�����A��B�غ�)����������ʼ�ճ�������____________��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
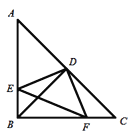
����Ŀ����ͼ���ı���ABCDΪƽ���ı������ӳ�AD��E��ʹDE=AD������EB��EC��DB������һ������������ʹ�ı���DBCE��Ϊ���ε����� ��

��A��AB=BE ��B��BE��DC ��C����ADB=90�� ��D��CE��DE
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �������
�������![]() ·�����յ�
·�����յ�![]() ��
��![]() ���ٶ��˶���ͬʱ��
���ٶ��˶���ͬʱ��![]() ��
��![]() �������
�������![]() ·�����յ�
·�����յ�![]() ��
��![]() ���ٶ��˶������㶼Ҫ������Ӧ���յ�ʱ����ֹͣ�˶�.�ֱ��
���ٶ��˶������㶼Ҫ������Ӧ���յ�ʱ����ֹͣ�˶�.�ֱ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����˶�ʱ��
�����˶�ʱ��![]() ____________
____________![]() ʱ��
ʱ��![]() ��ȥ
��ȥ![]() ȫ�ȣ�
ȫ�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪������ƽ���ϵ�![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() ����������
����������![]() ����
����![]() ��
��![]() ���㣮
���㣮

![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
![]() ������������ƽ�����ɸ���λ�õ�����������ǡ�þ�����
������������ƽ�����ɸ���λ�õ�����������ǡ�þ�����![]() �����������ߵĽ���ʽ��
�����������ߵĽ���ʽ��
![]() ��
��![]() �е�������Ķ���
�е�������Ķ���![]() �㣬
�㣬![]() Ϊ����������
����������![]() ����
����![]() ��֮���һ�㣬�Ե�
��֮���һ�㣬�Ե�![]() ΪԲ�Ļ�ͼ����
ΪԲ�Ļ�ͼ����![]() ��
��![]() ���ֱ��
���ֱ��![]() ������ʱ������
������ʱ������![]() ��
��![]() �����ı���
�����ı���![]() �������
�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com