
【题目】如图,已知直角坐标平面上的![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() ,
,![]() .若抛物线
.若抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.

![]() 求
求![]() 、
、![]() 的值;
的值;
![]() 将抛物线向上平移若干个单位得到的新抛物线恰好经过点
将抛物线向上平移若干个单位得到的新抛物线恰好经过点![]() ,求新抛物线的解析式;
,求新抛物线的解析式;
![]() 设
设![]() 中的新抛物的顶点
中的新抛物的顶点![]() 点,
点,![]() 为新抛物线上
为新抛物线上![]() 点至
点至![]() 点之间的一点,以点
点之间的一点,以点![]() 为圆心画图,当
为圆心画图,当![]() 与
与![]() 轴和直线
轴和直线![]() 都相切时,联结
都相切时,联结![]() 、
、![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】![]() ;
;![]() 新抛物线的解析式为
新抛物线的解析式为![]() ;
;![]() 四边形
四边形![]() 的面积为
的面积为![]() .
.
【解析】
(1)只需把点A、C的坐标代入抛物线的解析式就可解决问题;
(2)可设新抛物线的解析式为y=x2﹣2x﹣3+k,然后求出点B的坐标,并把点B的坐标代入新抛物线的解析式,就可解决问题;
(3)设⊙Q与x轴相切于点D,与直线BC相切于点E,连接QD、QE,易证四边形QECD是正方形,则有QD=DC.设点Q的横坐标为t,从而得到点Q的坐标为(t,3﹣t),代入新抛物线的解析式,求出点Q的坐标,然后运用割补法就可求出四边形ABQP的面积.
(1)∵抛物线y=ax2+bx﹣3经过A(﹣1,0)、C(3,0),∴![]() ,解得:
,解得:![]() ;
;
(2)设抛物线向上平移k个单位后得到的新抛物线恰好经过点B,则新抛物线的解析式为y=x2﹣2x﹣3+k.
∵A(﹣1,0)、C(3,0),∴CB=AC=3﹣(﹣1)=4.
∵∠ACB=90°,∴点B的坐标为(3,4).
∵点B(3,4)在抛物线y=x2﹣2x﹣3+k上,∴9﹣6﹣3+k=4,解得:k=4,∴新抛物线的解析式为y=x2﹣2x+1;
(3)设⊙Q与x轴相切于点D,与直线BC相切于点E,连接QD、QE,如图所示,则有QD⊥OC,QE⊥BC,QD=QE,∴∠QDC=∠DCE=∠QEC=90°,∴四边形QECD是矩形.
∵QD=QE,∴矩形QECD是正方形,∴QD=DC.
设点Q的横坐标为t,则有OD=t,QD=DC=OC﹣OD=3﹣t,∴点Q的坐标为(t,3﹣t).
∵点Q在抛物线y=x2﹣2x+1上,∴t2﹣2t+1=3﹣t,解得:t1=2,t2=﹣1.
∵Q为抛物线y=x2﹣2x+1上P点至B点之间的一点,∴t=2,点Q的坐标为(2,1),∴OD=2,QD=CD=1.
由y=x2﹣2x+1=(x﹣1)2得顶点P的坐标为(1,0),∴OP=1,PD=OD﹣OP=2﹣1=1,∴S四边形ABQP=S△ACB﹣S△PDQ﹣S梯形DQBC
=![]() ACBC﹣
ACBC﹣![]() PDQD﹣
PDQD﹣![]() (QD+BC)DC
(QD+BC)DC
=![]() ×4×4﹣
×4×4﹣![]() ×1×1﹣
×1×1﹣![]() ×(1+4)×1
×(1+4)×1
=5
∴四边形ABQP的面积为5.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校积极开展“阳光体育”活动,共开设了跳绳、足球、篮球、跑步四种运动项目.为了解学生最喜爱哪一种项目,童威随机抽取了部分学生进行调查,并绘制了如下的条形统计图和扇形统计图(部分信息未给出)
(1)本次被调查的学生人数为 ,扇形统计图中“跑步”所对的圆心角为 度.
(2)补全条形统计图;
(3)该校共有1200名学生,请估计全校最喜爱篮球的人数比最喜爱足球的人数多多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E, F在直线AC上,DF=BE, ∠AFD=∠CEB,下列条件中不能判断△ADF≌△CBE的是( )

A.∠D=∠BB.AD=CBC.AE=CFD.AD// BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为扩大销售增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价一元,市场每天可多售
元,为扩大销售增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价一元,市场每天可多售![]() 件,问他降价多少元时,才能使每天所赚的利润最大?并求出最大利润.
件,问他降价多少元时,才能使每天所赚的利润最大?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形的边长为1,点B、C的坐标分别为(-1, 3), (0, 1).
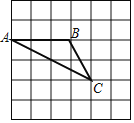
(1)建立符合条件的直角坐标系(要求标出x轴,y轴和原点),并写出点A的坐标
(2)线段AB上任意一点的坐标可以表示为
(3)在y轴上找到一点P,使得S△ABP = 3S△ABC,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 是第一、三象限的角平分线.
是第一、三象限的角平分线.

(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:![]() ___________、
___________、![]() ___________;
___________;
(2)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点![]() 关于第一、三象限的角平分线
关于第一、三象限的角平分线![]() 的对称点
的对称点![]() 的坐标为___________(不必证明);
的坐标为___________(不必证明);
(3)已知两点![]() 、
、![]() ,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.
,试在直线L上画出点Q,使点Q到D、E两点的距离之和最小,求QD+QE的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com