
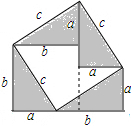
 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来证明a2+b2=c2.(请你写出证明过程)
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来证明a2+b2=c2.(请你写出证明过程)  新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{x}{2}$ | B. | $\frac{3}{x+1}$ | C. | $\frac{x}{2}+y$ | D. | $\frac{x}{π}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{{{(-3)}^2}}=3$ | B. | $\sqrt{36}$=±6 | C. | $\sqrt{3}+\sqrt{2}=\sqrt{5}$ | D. | $3+2\sqrt{3}=5\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| x | … | -3 | -2 | -1 | 1 | 2 | … |
| y | … | -6 | 0 | 4 | 6 | 4 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com