
| x | … | -3 | -2 | -1 | 1 | 2 | … |
| y | … | -6 | 0 | 4 | 6 | 4 | … |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用表中的对称点求得对称轴,利用对称性以及增减性逐项判定得出答案即可.
解答 解:∵抛物线经过点(-1,4),(2,4),
∴对称轴x=$\frac{-1+2}{2}$=$\frac{1}{2}$①错误;
∴(-2,0)的对称点为(3,0),也就是抛物线一定经过点(3,0)②正确;
∵在对称轴左侧y随着x的增大而增大,在对称轴右侧y随着x的增大而减小,
∴③是错误的;
∵点A(-$\frac{3}{4}$,y1)的对称点为A′($\frac{7}{4}$,y1),B($\frac{7}{5}$,y2),$\frac{7}{4}$>$\frac{7}{5}$>$\frac{1}{2}$,
∴y1<y2,④错误.
正确的只有1个.
故选:A.
点评 此题考查了二次函数的性质.要熟练掌握函数的特殊值对应的特殊点.解题关键是根据表格中数据找到对称性以及数据的特点求出对称轴,图象与x,y轴的交点坐标等.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -$\frac{1}{2}$ | C. | 1或-$\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
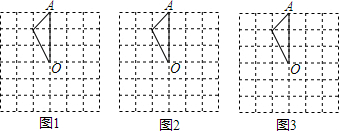
 (1)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).在图中作出△ABC关于y轴对称的△A1B1C1;
(1)如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).在图中作出△ABC关于y轴对称的△A1B1C1;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
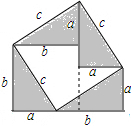 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来证明a2+b2=c2.(请你写出证明过程)
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来证明a2+b2=c2.(请你写出证明过程)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由3x-2=2x+1,移项得3x+2x=2+1 | |
| B. | 由$\frac{x-2}{2}$-$\frac{3x-2}{4}$=-1,去分母得2(x-2)-3x-2=-4 | |
| C. | 由2-3(x-1)=4,去括号得2-3x+3=4 | |
| D. | 由2x+3-x=5,合并同类项得3x+3=5. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com