
����Ŀ����ͼ����OAΪ�ߵ���OAB���Ϊ2�����е�B�ĺᡢ�������������4���Ҷ���С��0�������������У���ȷ���ǣ�_____������д��������ȷ��ѡ�
������B�ĺ�������4�������������ĵ�B����ֻ��1����
������B�����㣨���ᡢ�����궼���������������������ĵ�B��4����
��������ϵ�ڣ�����������������ĵ�B��һ������һ��C��ʹ����CAB����COA����COB�����ȣ�
��������ϵ�ڣ�����һ������D��ʹ�ö����������������ĵ�B����DBA����DBO�����ȣ�


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����C��AOB��һ��OA�ϣ�����C��ֱ��DE//OB��CFƽ��ACD��CG CF��C ��
��1����O =40����ECF�Ķ�����
��2����֤��CGƽ��OCD��
��3����OΪ���ٶ�ʱ��CDƽ��OCF����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������C1��y=x2+bx+c����ԭ�㣬��x�����һ������Ϊ��2��0������������C1����ƽ��m��m��0������λ�õ�������C2 �� C2��x����A��B���㣨��A�ڵ�B����ߣ�����y���ڵ�C��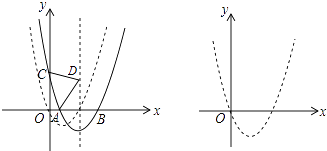
��1����������C1�Ľ���ʽ���������ꣻ
��2����ACΪб������������ֱ��������ACD������D����������C2�ĶԳ�����ʱ����������C2�Ľ���ʽ��
��3����������C2�ĶԳ�����ڵ�P��ʹ�� PACΪ�ȱ������Σ���m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��y=��x��y������ƽ�ƺ��ֱ��ǡ�þ�����A��2����4��������y�ύ�ڵ�B����x���ϴ���һ��Pʹ��PA+PB��ֵ��С�����P������Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�е�A��B���������ϣ�����A��0��a����B��b��0��������|a��3|+![]() ��0��
��0��

��1�����A��B�����ꣻ
��2����ABƽ�Ƶ�CD����A��Ӧ��C����2��m��������ABC���Ϊ13������CO�����C�����ꣻ
��3���ڣ�2���������£���֤����AOC����OAB+��OCD��
��4����ͼ2����AB��CD����C��DҲ���������ϣ���FΪ�߶�AB��һ���㣨������A��B���㣩������OF��FPƽ�֡�BFO����BCP��2��PCD����֤������COF��3��P����OFP����ʾ����ֱ�����ã�3���Ľ��ۣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
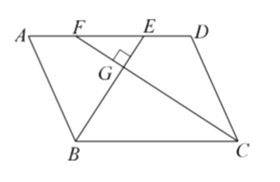
����Ŀ����ͼ�����ı���![]() �У�
�У�![]() ��ƽ���߽�
��ƽ���߽�![]() �ڵ�
�ڵ�![]() ��ƽ���߽�
��ƽ���߽�![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��
��1����֤���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��2����![]() �����߶�
�����߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�������ڼ�����������֯��һ�η����¹ڲ�����֪ʶ�����������صȽ�10�ˣ����㽱20�ˣ�ѧУ���������л�ѧ������һ�ݽ�Ʒ��ͬһ�ȴεĽ�Ʒ��ͬ��
��1�����з������Ӧ���⣩���صȽ������㽱�Ľ�Ʒ�ֱ��ǿ��ֺ��¶ȼƣ����ֵ��۵�2�����¶ȼƵ��۵�3����ȣ����������ֽ�Ʒһ������700Ԫ������ֺ��¶ȼƵĵ��۸��Ƕ���Ԫ��
��2�������ò���ʽ��ʽ���Ӧ���⣩�����ֽ�Ʒ�ĵ��۶�����������Ҫ���صȽ����۱����㽱���۶�20Ԫ�����ܷ��ò�����440������500Ԫ��ǰ���£����������ֽ�Ʒʱ���ǵĵ����м����������ֱ����ÿ������صȽ������㽱��Ʒ�ĵ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ļ��յ����۹���Ӧ��ij�յ����ӵ�һ�ݽ���������Ҫ����10���ڣ���10�죩�������Ϊ�������Ч�ʣ������Ӱ�ӵ㣬�ӵ�����ĵ�һ��������˿յ�42̨���Ժ�ÿ�������Ŀյ�����ǰһ���2̨�����ڻ�����ĵ�ԭ���������Ŀյ������ﵽ50̨��ÿ������һ̨���������������пյ���ƽ��ÿ̨�ɱ�������20Ԫ��
��1�����x�������յ�y̨��ֱ��д��y��x֮��ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
��2����ÿ̨�յ��ijɱ��ۣ���������������50̨ʱ��Ϊ2000Ԫ�������۸�Ϊÿ̨2920Ԫ�����x�������ΪWԪ������W��x֮��ĺ�������ʽ��������һ���õ����������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
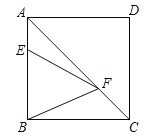
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() �ǶԽ���
�ǶԽ���![]() �ϵ�һ�����㣬��
�ϵ�һ�����㣬��![]() ����Сֵ��10����
����Сֵ��10����![]() ��Ϊ___________��
��Ϊ___________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com