
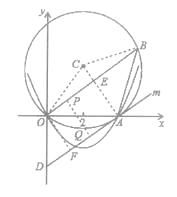
����Ŀ����ͼ��C���ڽӡ�AOB�У�AB=AO=4��tan��AOB= ![]() ��������y=ax2+bx������A��4,0����㣨-2,6��.
��������y=ax2+bx������A��4,0����㣨-2,6��.
��1���������ߵĺ�������ʽ��
��2��ֱ��m��C�����ڵ�A����y���ڵ�D����֤��AD//OB��
��3���ڣ�2���������£���P���߶�OB�ϣ��ӵ�O�������B�˶���ͬʱ����Q���߶�DA�ϣ��ӵ�D�������A�˶�����P���ٶ�Ϊÿ��1����λ������Q���ٶ�Ϊÿ��2����λ������PQ��ADʱ�����˶�ʱ��t��ֵ.
���𰸡�
��1��
�⣺��������y=ax2+bx������A��4,0����㣨-2,6����
�� ![]()
��� 
���������ߵĽ���ʽΪy= ![]() .
.
��2��
�⣺��ͼ������AC��OB�ڵ�E������OC��BC��
��OC=BC��AB=AO��
��AC��OB��
��ADΪ���ߣ�
��AC��AD��
��AD//OB.
��3��
�⣺��tan��AOB= ![]() ��
��
��sin��AOB= ![]() ��
��
��AE=OA��sin��AOB=4�� ![]() =2.4��
=2.4��
��AD//OB��
���OAD=��AOB��
��OD=OA��tan��OAD=OA��tan��AOB=4�� ![]() =3��
=3��
��PQ��ADʱ��OP=t��DQ=2t��
��O����OF��AD��F��
��Rt��ODF��OD=3��OF=AE=2.4��DF=DQ-FQ=DQ-OP=2t-t=t��
�ɹ��ɶ����ã�DF= ![]() =
= ![]() =1.8��
=1.8��
��t=1.8��.
����������1���������������뺯������ʽ�����a��b��ֵ���ɣ���2������AC��OB�ڵ�E������OC��BC������AO=AB�����ݡ������������ɵ�Aƽ�ֻ�OB����AC��OB������ADΪ���ߣ���AC��AD����AD//OB.��3��OP=t��DQ=2t���ɹ�O����OF��AD��F����DF=DQ-FQ=DQ-OP=2t-t=t������ֻҪ���DF���ɣ�����tan��AOB= ![]() ����AD//OB��AO=4�����.
����AD//OB��AO=4�����.
�����㾫����������Ŀ����֪���������ö��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����MON=20�㣬A��B�ֱ�Ϊ����OM��ON�������㣬��OA=2��OB=4����P��Q�ֱ�Ϊ����OM��ON�����㣬��P��Q�˶�ʱ���߶�AQ+PQ+PB����Сֵ�ǣ� �� 
A.3
B.3 ![]()
C.2
D.2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��y=��2x+b��b��0����λ����b�IJ�ͬȡֵ���仯��
��1����֪��M��Բ������Ϊ��4��2�����뾶Ϊ2��
��b=ʱ��ֱ��l��y=��2x+b��b��0������Բ��M��
��b=ʱ��ֱ��l��y=��2x+b��b��0�����M���У�
��2�����ѡ�M���ɾ���ABCD����������������ֱ�Ϊ��A��2��0����B��6��0����C��6��2������ֱ��lɨ������ABCD�����ΪS����b��С����仯ʱ�������S��b�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y=��x��2�뷴��������y= ![]() ��ͼ����A��B���㣬����x��y�ύ��C��D���㣬A�������Ϊ����3��k+4����
��ͼ����A��B���㣬����x��y�ύ��C��D���㣬A�������Ϊ����3��k+4����
��1�����������Ľ���ʽ
��2����ֱ��AB���ŵ�M����1����1��˳ʱ����ת��MN��ʹֱ��MN��x�ᣬ���뷴����������ͼ���ڵ�N������ת�Ǵ�С���߶�MN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AEƽ�֡�BAD��BC��E����CAE=15�㣬�����н��ۣ�
�١�ODC�ǵȱ������� ��BC=2AB �ۡ�AOE=135�� ��S��AOE=S��COE
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ڼ�¥A�����⿴�������ܵ�ǰ����¥���ڵ������ֻ�ܿ�������D��������Ϊ����Сӱ�ڼ�¥B����B��A�����·������⿴������ܿ�������E��������Ϊ�£�������G��F��D��E��ͬһֱ���ϣ���֪��¥��CFΪ10m��������¥���FGΪ15m�����Ǧ�=45�㣬��=35�㣮
��1�����A������ľ���AG��
��2����A��B֮��ľ��룮(�����ȷ��0.1m)��sin35���0.57��cos35���0.82��tan35���0.70��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Сǿϴ��ʱ�IJ���ʾ��ͼ��ϴ��̨������ ![]() ����ǽ�ڷţ���
����ǽ�ڷţ��� ![]() ����
���� ![]() ��Сǿ����
��Сǿ���� ![]() ���°���
���°��� ![]() ��ϴ��ʱ�°���������
��ϴ��ʱ�°��������� ![]() ��
�� ![]() ��������ǰ���
��������ǰ��� ![]() ��
�� ![]() ��������ϴ��̨����
��������ϴ��̨���� ![]() ����
���� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��ͬһֱ���ϣ���
��ͬһֱ���ϣ���
��1����ʱСǿͷ�� ![]() �������
������� ![]() �����٣�
�����٣�
��2��Сǿϣ������ͷ�� ![]() ǡ����ϴ����
ǡ����ϴ���� ![]() ���е�
���е� ![]() �����Ϸ�����Ӧ��ǰ����˶��٣�
�����Ϸ�����Ӧ��ǰ����˶��٣�
�� ![]() ��
�� ![]() ��
�� ![]() �������ȷ��
�������ȷ�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ���������½��ۣ� ��2a��b=0��
��9a+3b+c��0��
�۹���x��һԪ���η���ax2+bx+c+3=0���������ʵ������
��8a+c��0��
������ȷ�ĸ����ǣ� ��
A.2
B.3
C.4
D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ȱ�������ABC�У���D��E��F���ֱ�Ϊ��AB��AC��BC���е㣬MΪֱ��BC���㣬��DMNΪ�ȱ�������
��1����ͼ1������M�ڵ�B���ʱ�������ж�EN��MF��������������ϵ��
��2����ͼ2������M��BC��ʱ�������������䣬��1���Ľ�����EN��MF��������ϵ�Ƿ���Ȼ��������������������ͼ2֤��������������˵�����ɣ�
��3������M�ڵ�C�Ҳ�ʱ��������ͼ3�л�����Ӧ��ͼ�Σ����жϣ�1���Ľ����Ƿ���Ȼ����������������ֱ��д�����ۣ�����������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com